Sunan Huang
Receding Horizon Motion Planning for Multi-Agent Systems: A Velocity Obstacle Based Probabilistic Method
Mar 24, 2021
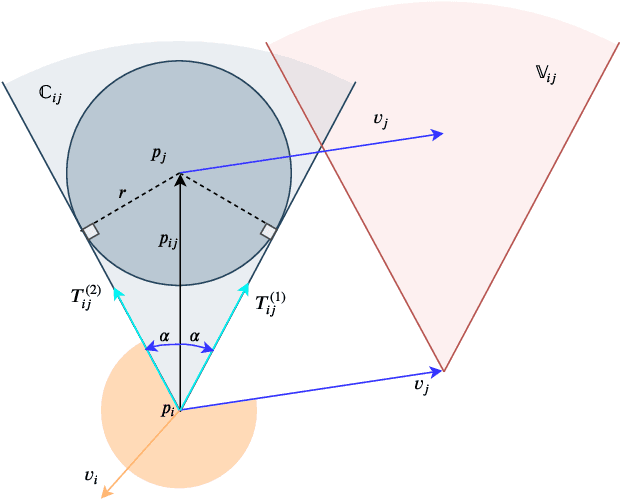
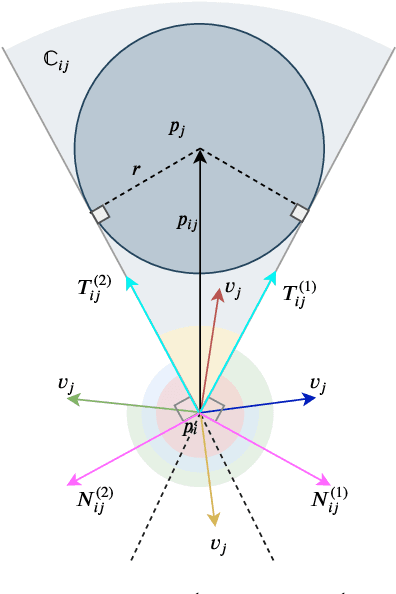
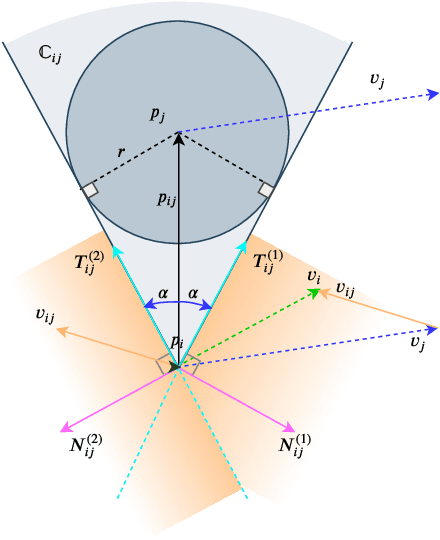
Abstract:In this paper, a novel and innovative methodology for feasible motion planning in the multi-agent system is developed. On the basis of velocity obstacles characteristics, the chance constraints are formulated in the receding horizon control (RHC) problem, and geometric information of collision cones is used to generate the feasible regions of velocities for the host agent. By this approach, the motion planning is conducted at the velocity level instead of the position level. Thus, it guarantees a safer collision-free trajectory for the multi-agent system, especially for the systems with high-speed moving agents. Moreover, a probability threshold of potential collisions can be satisfied during the motion planning process. In order to validate the effectiveness of the methodology, different scenarios for multiple agents are investigated, and the simulation results clearly show that the proposed approach can effectively avoid potential collisions with a collision probability less than a specific threshold.
Accelerated Hierarchical ADMM for Nonconvex Optimization in Multi-Agent Decision Making
Nov 01, 2020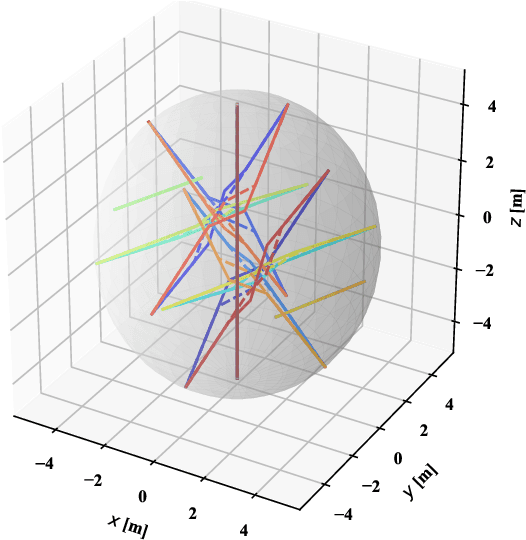
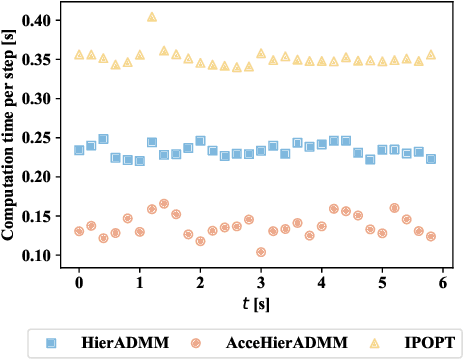
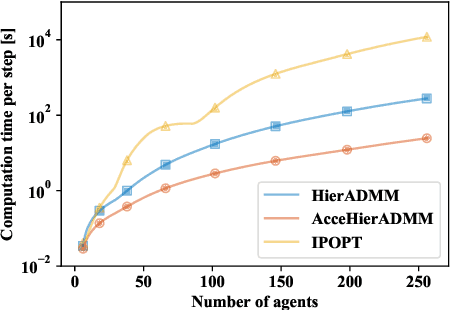
Abstract:Distributed optimization is widely used to solve large-scale problems effectively in a localized and coordinated manner. Thus, it is noteworthy that the methodology of distributed model predictive control (DMPC) has become a promising approach to achieve effective outcomes; and particularly in decision-making tasks for multi-agent systems. However, the typical deployment of such DMPC frameworks would lead to involvement of nonlinear processes with a large number of nonconvex constraints. Noting all these attendant constraints and limitations, the development and innovation of a hierarchical three-block alternating direction method of multipliers (ADMM) approach is presented in the work here to solve the nonconvex optimization problem that arises for such a decision-making problem in multi-agent systems. Firstly thus, an additional slack variable is introduced to relax the original large-scale nonconvex optimization problem; such that the intractable nonconvex coupling constraints are suitably related to the distributed agents. Then, the approach with a hierarchical ADMM that contains outer loop iteration by the augmented Lagrangian method (ALM), and inner loop iteration by three-block semi-proximal ADMM, is utilized to solve the resulting relaxed nonconvex optimization problem. Additionally, it is shown that the appropriate desired stationary point exists for the procedures of the hierarchical stages for convergence in the algorithm. Next, the approximate optimization with a barrier method is then applied to accelerate the computational efficiency. Finally, a multi-agent system involving decision-making for multiple unmanned aerial vehicles (UAVs) is utilized to demonstrate the effectiveness of the proposed method in terms of attained performance and computational efficiency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge