Accelerated Hierarchical ADMM for Nonconvex Optimization in Multi-Agent Decision Making

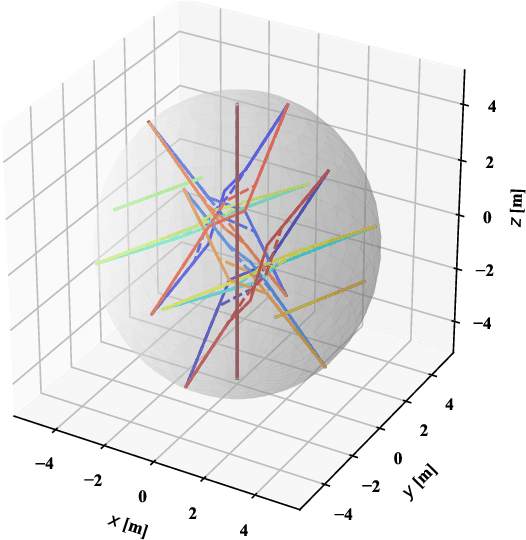
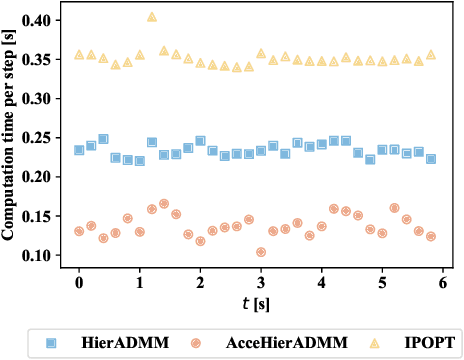
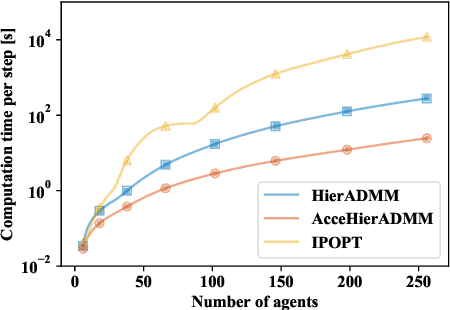
Distributed optimization is widely used to solve large-scale problems effectively in a localized and coordinated manner. Thus, it is noteworthy that the methodology of distributed model predictive control (DMPC) has become a promising approach to achieve effective outcomes; and particularly in decision-making tasks for multi-agent systems. However, the typical deployment of such DMPC frameworks would lead to involvement of nonlinear processes with a large number of nonconvex constraints. Noting all these attendant constraints and limitations, the development and innovation of a hierarchical three-block alternating direction method of multipliers (ADMM) approach is presented in the work here to solve the nonconvex optimization problem that arises for such a decision-making problem in multi-agent systems. Firstly thus, an additional slack variable is introduced to relax the original large-scale nonconvex optimization problem; such that the intractable nonconvex coupling constraints are suitably related to the distributed agents. Then, the approach with a hierarchical ADMM that contains outer loop iteration by the augmented Lagrangian method (ALM), and inner loop iteration by three-block semi-proximal ADMM, is utilized to solve the resulting relaxed nonconvex optimization problem. Additionally, it is shown that the appropriate desired stationary point exists for the procedures of the hierarchical stages for convergence in the algorithm. Next, the approximate optimization with a barrier method is then applied to accelerate the computational efficiency. Finally, a multi-agent system involving decision-making for multiple unmanned aerial vehicles (UAVs) is utilized to demonstrate the effectiveness of the proposed method in terms of attained performance and computational efficiency.