Understanding Hallucinations in Diffusion Models through Mode Interpolation

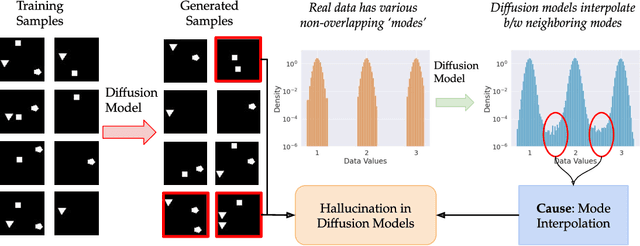
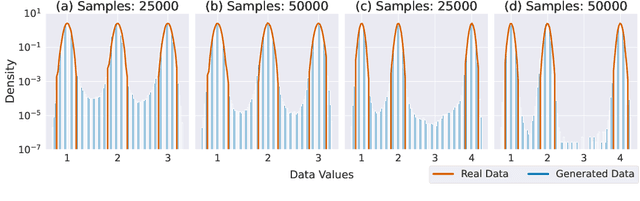
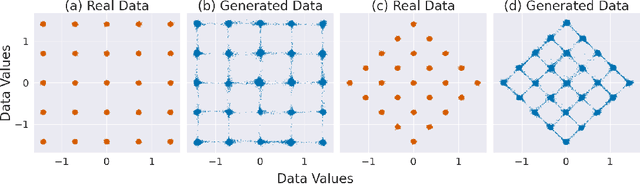
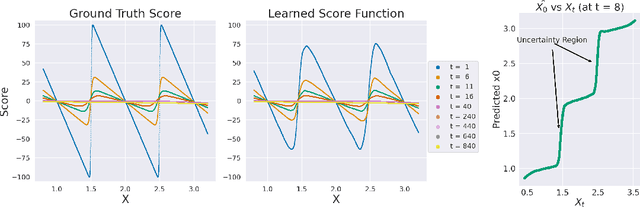
Colloquially speaking, image generation models based upon diffusion processes are frequently said to exhibit "hallucinations," samples that could never occur in the training data. But where do such hallucinations come from? In this paper, we study a particular failure mode in diffusion models, which we term mode interpolation. Specifically, we find that diffusion models smoothly "interpolate" between nearby data modes in the training set, to generate samples that are completely outside the support of the original training distribution; this phenomenon leads diffusion models to generate artifacts that never existed in real data (i.e., hallucinations). We systematically study the reasons for, and the manifestation of this phenomenon. Through experiments on 1D and 2D Gaussians, we show how a discontinuous loss landscape in the diffusion model's decoder leads to a region where any smooth approximation will cause such hallucinations. Through experiments on artificial datasets with various shapes, we show how hallucination leads to the generation of combinations of shapes that never existed. Finally, we show that diffusion models in fact know when they go out of support and hallucinate. This is captured by the high variance in the trajectory of the generated sample towards the final few backward sampling process. Using a simple metric to capture this variance, we can remove over 95% of hallucinations at generation time while retaining 96% of in-support samples. We conclude our exploration by showing the implications of such hallucination (and its removal) on the collapse (and stabilization) of recursive training on synthetic data with experiments on MNIST and 2D Gaussians dataset. We release our code at https://github.com/locuslab/diffusion-model-hallucination.

Escaping Saddle Points for Effective Generalization on Class-Imbalanced Data

Real-world datasets exhibit imbalances of varying types and degrees. Several techniques based on re-weighting and margin adjustment of loss are often used to enhance the performance of neural networks, particularly on minority classes. In this work, we analyze the class-imbalanced learning problem by examining the loss landscape of neural networks trained with re-weighting and margin-based techniques. Specifically, we examine the spectral density of Hessian of class-wise loss, through which we observe that the network weights converge to a saddle point in the loss landscapes of minority classes. Following this observation, we also find that optimization methods designed to escape from saddle points can be effectively used to improve generalization on minority classes. We further theoretically and empirically demonstrate that Sharpness-Aware Minimization (SAM), a recent technique that encourages convergence to a flat minima, can be effectively used to escape saddle points for minority classes. Using SAM results in a 6.2\% increase in accuracy on the minority classes over the state-of-the-art Vector Scaling Loss, leading to an overall average increase of 4\% across imbalanced datasets. The code is available at: https://github.com/val-iisc/Saddle-LongTail.

A Closer Look at Smoothness in Domain Adversarial Training

Domain adversarial training has been ubiquitous for achieving invariant representations and is used widely for various domain adaptation tasks. In recent times, methods converging to smooth optima have shown improved generalization for supervised learning tasks like classification. In this work, we analyze the effect of smoothness enhancing formulations on domain adversarial training, the objective of which is a combination of task loss (eg. classification, regression, etc.) and adversarial terms. We find that converging to a smooth minima with respect to (w.r.t.) task loss stabilizes the adversarial training leading to better performance on target domain. In contrast to task loss, our analysis shows that converging to smooth minima w.r.t. adversarial loss leads to sub-optimal generalization on the target domain. Based on the analysis, we introduce the Smooth Domain Adversarial Training (SDAT) procedure, which effectively enhances the performance of existing domain adversarial methods for both classification and object detection tasks. Our analysis also provides insight into the extensive usage of SGD over Adam in the community for domain adversarial training.

S$^3$VAADA: Submodular Subset Selection for Virtual Adversarial Active Domain Adaptation

Unsupervised domain adaptation (DA) methods have focused on achieving maximal performance through aligning features from source and target domains without using labeled data in the target domain. Whereas, in the real-world scenario's it might be feasible to get labels for a small proportion of target data. In these scenarios, it is important to select maximally-informative samples to label and find an effective way to combine them with the existing knowledge from source data. Towards achieving this, we propose S$^3$VAADA which i) introduces a novel submodular criterion to select a maximally informative subset to label and ii) enhances a cluster-based DA procedure through novel improvements to effectively utilize all the available data for improving generalization on target. Our approach consistently outperforms the competing state-of-the-art approaches on datasets with varying degrees of domain shifts.