Soft Gradient Boosting with Learnable Feature Transforms for Sequential Regression

We propose a soft gradient boosting framework for sequential regression that embeds a learnable linear feature transform within the boosting procedure. At each boosting iteration, we train a soft decision tree and learn a linear input feature transform Q together. This approach is particularly advantageous in high-dimensional, data-scarce scenarios, as it discovers the most relevant input representations while boosting. We demonstrate, using both synthetic and real-world datasets, that our method effectively and efficiently increases the performance by an end-to-end optimization of feature selection/transform and boosting while avoiding overfitting. We also extend our algorithm to differentiable non-linear transforms if overfitting is not a problem. To support reproducibility and future work, we share our code publicly.

Fitting Multiple Machine Learning Models with Performance Based Clustering

Traditional machine learning approaches assume that data comes from a single generating mechanism, which may not hold for most real life data. In these cases, the single mechanism assumption can result in suboptimal performance. We introduce a clustering framework that eliminates this assumption by grouping the data according to the relations between the features and the target values and we obtain multiple separate models to learn different parts of the data. We further extend our framework to applications having streaming data where we produce outcomes using an ensemble of models. For this, the ensemble weights are updated based on the incoming data batches. We demonstrate the performance of our approach over the widely-studied real life datasets, showing significant improvements over the traditional single-model approaches.

Context-Aware Ensemble Learning for Time Series

We investigate ensemble methods for prediction in an online setting. Unlike all the literature in ensembling, for the first time, we introduce a new approach using a meta learner that effectively combines the base model predictions via using a superset of the features that is the union of the base models' feature vectors instead of the predictions themselves. Here, our model does not use the predictions of the base models as inputs to a machine learning algorithm, but choose the best possible combination at each time step based on the state of the problem. We explore three different constraint spaces for the ensembling of the base learners that linearly combines the base predictions, which are convex combinations where the components of the ensembling vector are all nonnegative and sum up to 1; affine combinations where the weight vector components are required to sum up to 1; and the unconstrained combinations where the components are free to take any real value. The constraints are both theoretically analyzed under known statistics and integrated into the learning procedure of the meta learner as a part of the optimization in an automated manner. To show the practical efficiency of the proposed method, we employ a gradient-boosted decision tree and a multi-layer perceptron separately as the meta learners. Our framework is generic so that one can use other machine learning architectures as the ensembler as long as they allow for a custom differentiable loss for minimization. We demonstrate the learning behavior of our algorithm on synthetic data and the significant performance improvements over the conventional methods over various real life datasets, extensively used in the well-known data competitions. Furthermore, we openly share the source code of the proposed method to facilitate further research and comparison.

Crime Prediction with Graph Neural Networks and Multivariate Normal Distributions

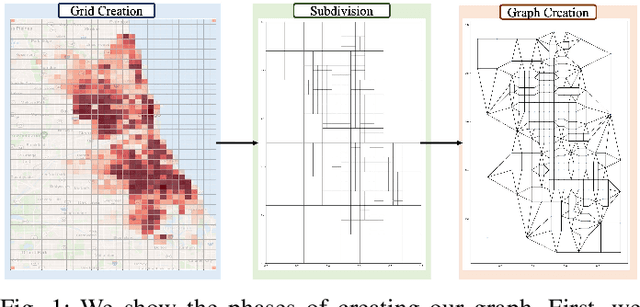
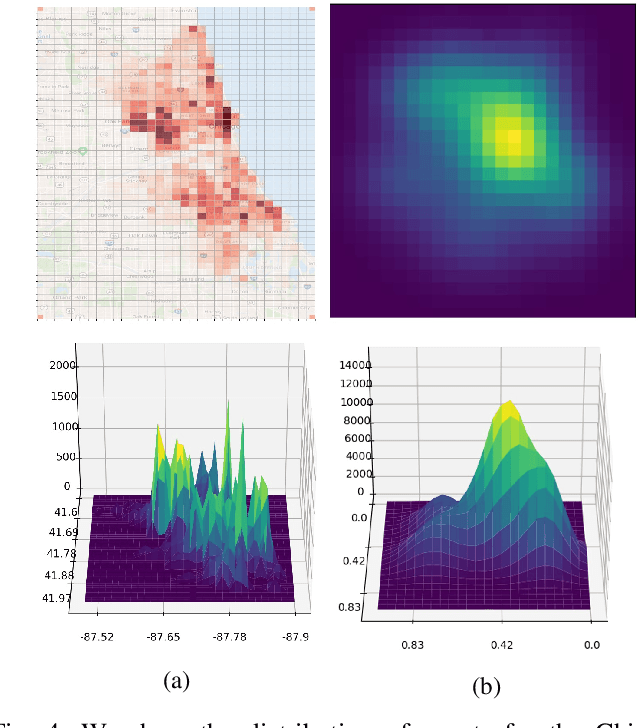
Existing approaches to the crime prediction problem are unsuccessful in expressing the details since they assign the probability values to large regions. This paper introduces a new architecture with the graph convolutional networks (GCN) and multivariate Gaussian distributions to perform high-resolution forecasting that applies to any spatiotemporal data. We tackle the sparsity problem in high resolution by leveraging the flexible structure of GCNs and providing a subdivision algorithm. We build our model with Graph Convolutional Gated Recurrent Units (Graph-ConvGRU) to learn spatial, temporal, and categorical relations. In each node of the graph, we learn a multivariate probability distribution from the extracted features of GCNs. We perform experiments on real-life and synthetic datasets, and our model obtains the best validation and the best test score among the baseline models with significant improvements. We show that our model is not only generative but also precise.

Spatio-temporal Weather Forecasting and Attention Mechanism on Convolutional LSTMs

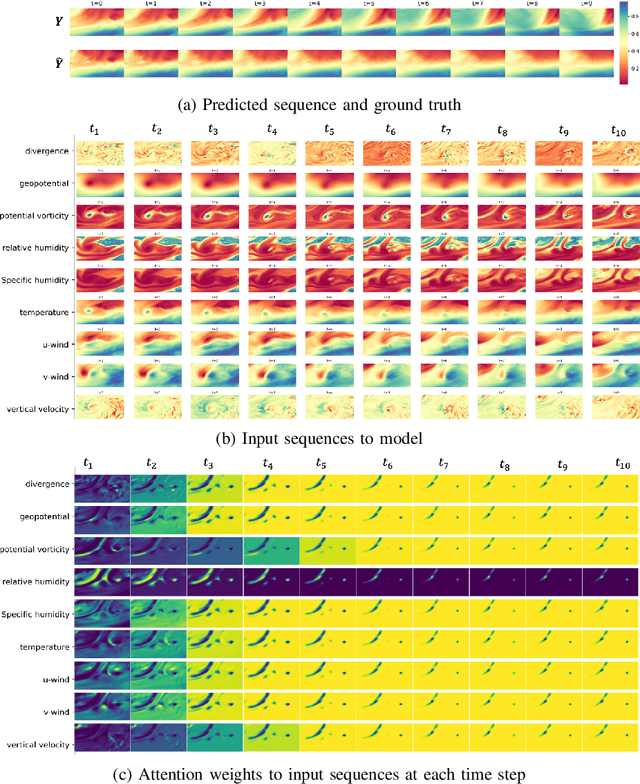
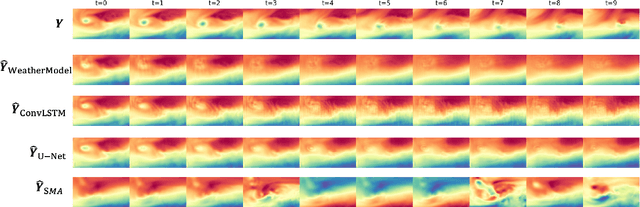
Numerical weather forecasting on high-resolution physical models consume hours of computations on supercomputers. Application of deep learning and machine learning methods in forecasting revealed new solutions in this area. In this paper, we forecast high-resolution numeric weather data using both input weather data and observations by providing a novel deep learning architecture. We formulate the problem as spatio-temporal prediction. Our model is composed of Convolutional Long-short Term Memory, and Convolutional Neural Network units with encoder-decoder structure. We enhance the short-long term performance and interpretability with an attention and a context matcher mechanism. We perform experiments on high-scale, real-life, benchmark numerical weather dataset, ERA5 hourly data on pressure levels, and forecast the temperature. The results show significant improvements in capturing both spatial and temporal correlations with attention matrices focusing on different parts of the input series. Our model obtains the best validation and the best test score among the baseline models, including ConvLSTM forecasting network and U-Net. We provide qualitative and quantitative results and show that our model forecasts 10 time steps with 3 hour frequency with an average of 2 degrees error. Our code and the data are publicly available.

Markovian RNN: An Adaptive Time Series Prediction Network with HMM-based Switching for Nonstationary Environments

We investigate nonlinear regression for nonstationary sequential data. In most real-life applications such as business domains including finance, retail, energy and economy, timeseries data exhibits nonstationarity due to the temporally varying dynamics of the underlying system. We introduce a novel recurrent neural network (RNN) architecture, which adaptively switches between internal regimes in a Markovian way to model the nonstationary nature of the given data. Our model, Markovian RNN employs a hidden Markov model (HMM) for regime transitions, where each regime controls hidden state transitions of the recurrent cell independently. We jointly optimize the whole network in an end-to-end fashion. We demonstrate the significant performance gains compared to vanilla RNN and conventional methods such as Markov Switching ARIMA through an extensive set of experiments with synthetic and real-life datasets. We also interpret the inferred parameters and regime belief values to analyze the underlying dynamics of the given sequences.

Unsupervised Online Anomaly Detection On Irregularly Sampled Or Missing Valued Time-Series Data Using LSTM Networks

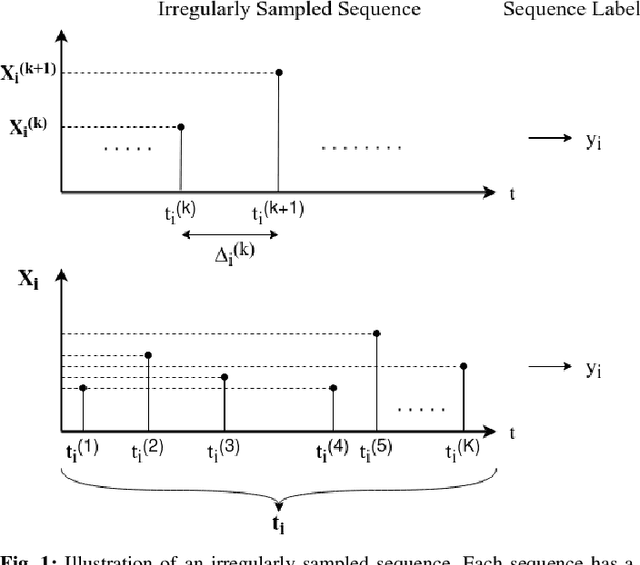
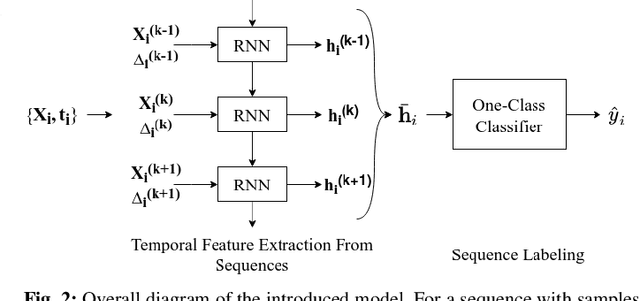
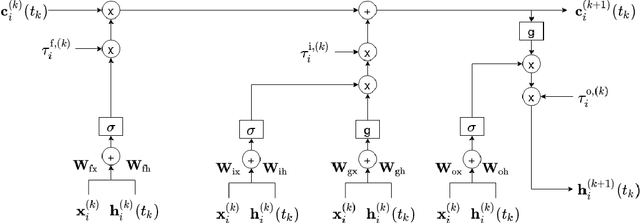
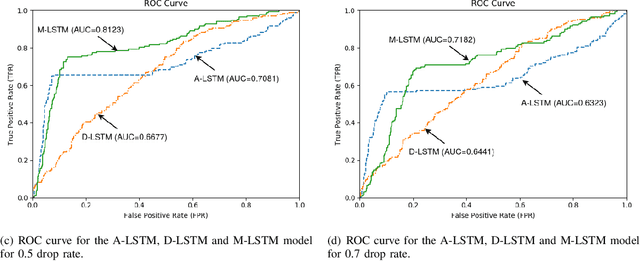
We study anomaly detection and introduce an algorithm that processes variable length, irregularly sampled sequences or sequences with missing values. Our algorithm is fully unsupervised, however, can be readily extended to supervised or semisupervised cases when the anomaly labels are present as remarked throughout the paper. Our approach uses the Long Short Term Memory (LSTM) networks in order to extract temporal features and find the most relevant feature vectors for anomaly detection. We incorporate the sampling time information to our model by modulating the standard LSTM model with time modulation gates. After obtaining the most relevant features from the LSTM, we label the sequences using a Support Vector Data Descriptor (SVDD) model. We introduce a loss function and then jointly optimize the feature extraction and sequence processing mechanisms in an end-to-end manner. Through this joint optimization, the LSTM extracts the most relevant features for anomaly detection later to be used in the SVDD, hence completely removes the need for feature selection by expert knowledge. Furthermore, we provide a training algorithm for the online setup, where we optimize our model parameters with individual sequences as the new data arrives. Finally, on real-life datasets, we show that our model significantly outperforms the standard approaches thanks to its combination of LSTM with SVDD and joint optimization.

Modeling of Spatio-Temporal Hawkes Processes with Randomized Kernels

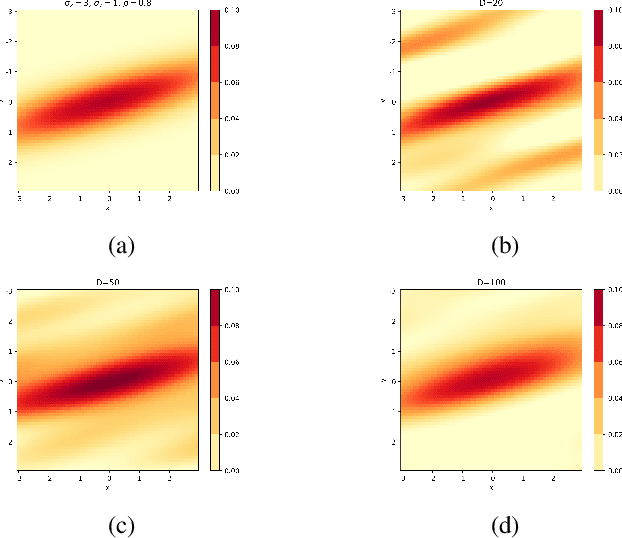
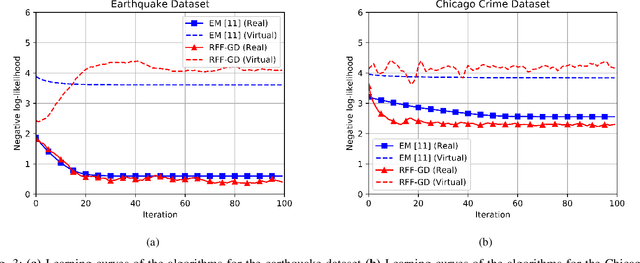
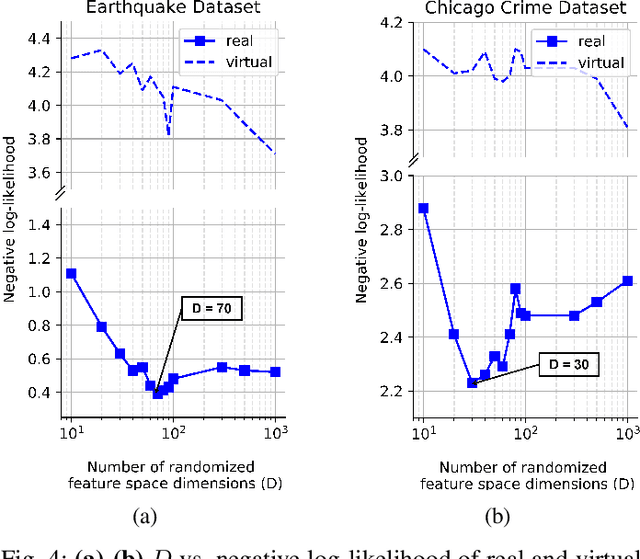
We investigate spatio-temporal event analysis using point processes. Inferring the dynamics of event sequences spatiotemporally has many practical applications including crime prediction, social media analysis, and traffic forecasting. In particular, we focus on spatio-temporal Hawkes processes that are commonly used due to their capability to capture excitations between event occurrences. We introduce a novel inference framework based on randomized transformations and gradient descent to learn the process. We replace the spatial kernel calculations by randomized Fourier feature-based transformations. The introduced randomization by this representation provides flexibility while modeling the spatial excitation between events. Moreover, the system described by the process is expressed within closed-form in terms of scalable matrix operations. During the optimization, we use maximum likelihood estimation approach and gradient descent while properly handling positivity and orthonormality constraints. The experiment results show the improvements achieved by the introduced method in terms of fitting capability in synthetic and real datasets with respect to the conventional inference methods in the spatio-temporal Hawkes process literature. We also analyze the triggering interactions between event types and how their dynamics change in space and time through the interpretation of learned parameters.

Prediction with Spatio-temporal Point Processes with Self Organizing Decision Trees

We study the spatio-temporal prediction problem, which has attracted attention of many researchers due to its critical real-life applications. In particular, we introduce a novel approach to this problem. Our approach is based on the Hawkes process, which is a non-stationary and self-exciting point process. We extend the formulations of a standard point process model that can represent time-series data to represent a spatio-temporal data. We model the data as nonstationary in time and space. Furthermore, we partition the spatial region we are working on into subregions via an adaptive decision tree and model the source statistics in each subregion with individual but mutually interacting point processes. We also provide a gradient based joint optimization algorithm for the point process and decision tree parameters. Thus, we introduce a model that can jointly infer the source statistics and an adaptive partitioning of the spatial region. Finally, we provide experimental results on a real-life data, which provides significant improvement due to space adaptation and joint optimization compared to standard well-known methods in the literature.

Accelerating Min-Max Optimization with Application to Minimal Bounding Sphere

We study the min-max optimization problem where each function contributing to the max operation is strongly-convex and smooth with bounded gradient in the search domain. By smoothing the max operator, we show the ability to achieve an arbitrarily small positive optimality gap of $\delta$ in $\tilde{O}(1/\sqrt{\delta})$ computational complexity (up to logarithmic factors) as opposed to the state-of-the-art strong-convexity computational requirement of $O(1/\delta)$. We apply this important result to the well-known minimal bounding sphere problem and demonstrate that we can achieve a $(1+\varepsilon)$-approximation of the minimal bounding sphere, i.e. identify an hypersphere enclosing a total of $n$ given points in the $d$ dimensional unbounded space $\mathbb{R}^d$ with a radius at most $(1+\varepsilon)$ times the actual minimal bounding sphere radius for an arbitrarily small positive $\varepsilon$, in $\tilde{O}(n d /\sqrt{\varepsilon})$ computational time as opposed to the state-of-the-art approach of core-set methodology, which needs $O(n d /\varepsilon)$ computational time.