Steven Wheelwright
Learning Reciprocity in Complex Sequential Social Dilemmas
Mar 19, 2019
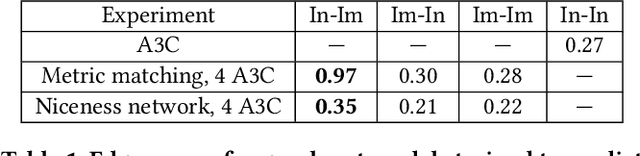

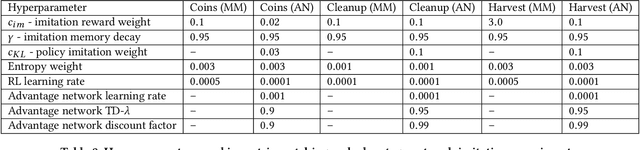
Abstract:Reciprocity is an important feature of human social interaction and underpins our cooperative nature. What is more, simple forms of reciprocity have proved remarkably resilient in matrix game social dilemmas. Most famously, the tit-for-tat strategy performs very well in tournaments of Prisoner's Dilemma. Unfortunately this strategy is not readily applicable to the real world, in which options to cooperate or defect are temporally and spatially extended. Here, we present a general online reinforcement learning algorithm that displays reciprocal behavior towards its co-players. We show that it can induce pro-social outcomes for the wider group when learning alongside selfish agents, both in a $2$-player Markov game, and in $5$-player intertemporal social dilemmas. We analyse the resulting policies to show that the reciprocating agents are strongly influenced by their co-players' behavior.
Malthusian Reinforcement Learning
Dec 17, 2018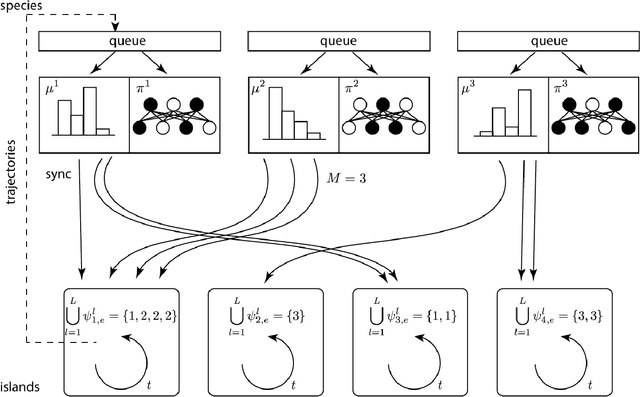
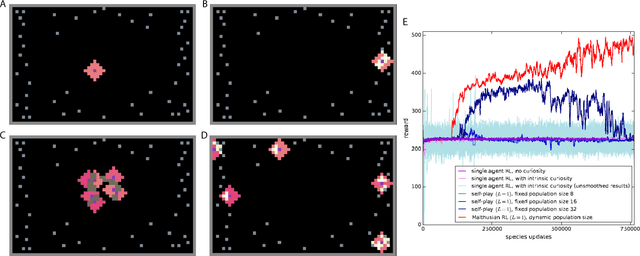
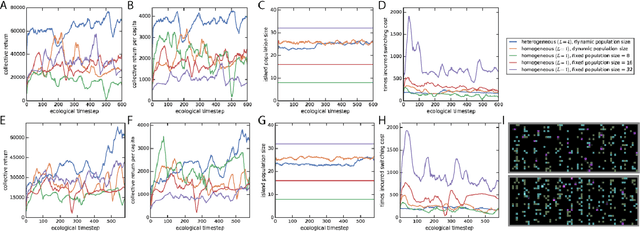
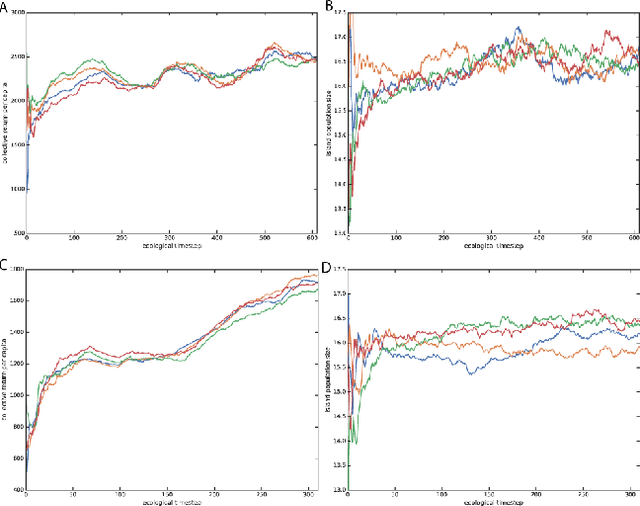
Abstract:Here we explore a new algorithmic framework for multi-agent reinforcement learning, called Malthusian reinforcement learning, which extends self-play to include fitness-linked population size dynamics that drive ongoing innovation. In Malthusian RL, increases in a subpopulation's average return drive subsequent increases in its size, just as Thomas Malthus argued in 1798 was the relationship between preindustrial income levels and population growth. Malthusian reinforcement learning harnesses the competitive pressures arising from growing and shrinking population size to drive agents to explore regions of state and policy spaces that they could not otherwise reach. Furthermore, in environments where there are potential gains from specialization and division of labor, we show that Malthusian reinforcement learning is better positioned to take advantage of such synergies than algorithms based on self-play.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge