Constructing High-Order Signed Distance Maps from Computed Tomography Data with Application to Bone Morphometry

An algorithm is presented for constructing high-order signed distance fields for two phase materials imaged with computed tomography. The signed distance field is high-order in that it is free of the quantization artifact associated with the distance transform of sampled signals. The narrowband is solved using a closest point algorithm extended for implicit embeddings that are not a signed distance field. The high-order fast sweeping algorithm is used to extend the narrowband to the remainder of the domain. The order of accuracy of the narrowband and extension methods are verified on ideal implicit surfaces. The method is applied to ten excised cubes of bovine trabecular bone. Localization of the surface, estimation of phase densities, and local morphometry is validated with these subjects. Since the embedding is high-order, gradients and thus curvatures can be accurately estimated locally in the image data.

High-Order Signed Distance Transform of Sampled Signals

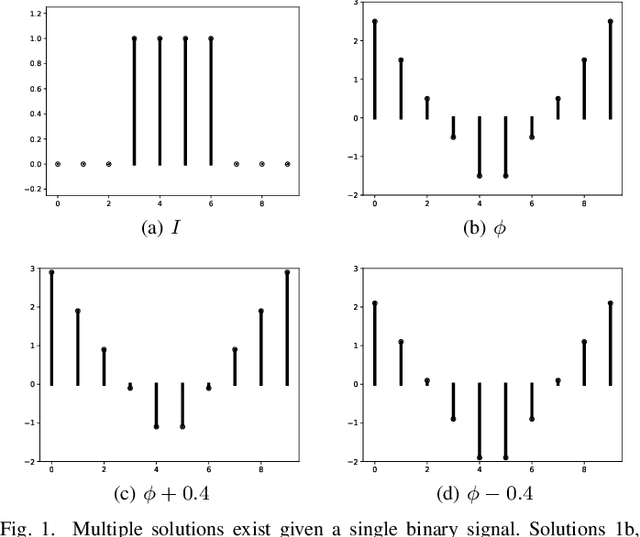
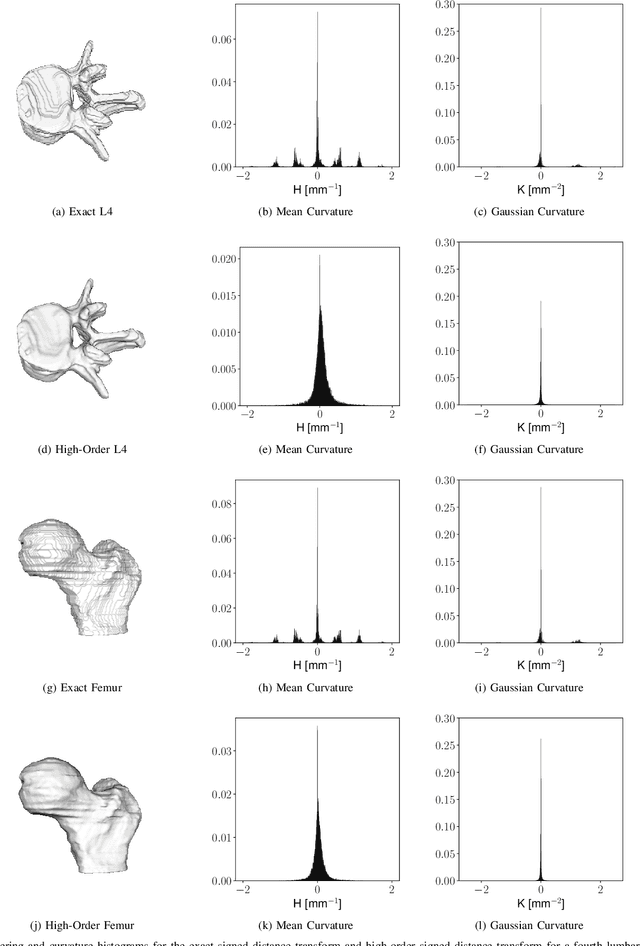
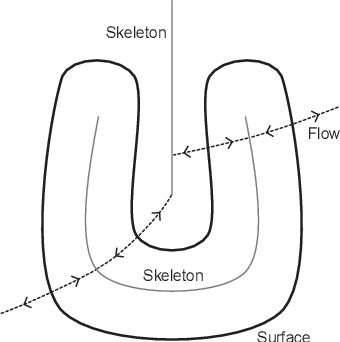
Signed distance transforms of sampled signals can be constructed better than the traditional exact signed distance transform. Such a transform is termed the high-order signed distance transform and is defined as satisfying three conditions: the Eikonal equation, recovery by a Heaviside function, and has an order of accuracy greater than unity away from the medial axis. Such a transform is an improvement to the classic notion of an exact signed distance transform because it does not exhibit artifacts of quantization. A large constant, linear time complexity high-order signed distance transform for arbitrary dimensionality sampled signals is developed based on the high order fast sweeping method. The transform is initialized with an exact signed distance transform and quantization corrected through an upwind solver for the boundary value Eikonal equation. The proposed method cannot attain arbitrary order of accuracy and is limited by the initialization method and non-uniqueness of the problem. However, meshed surfaces are visually smoother and do not exhibit artifacts of quantization in local mean and Gaussian curvature.

Local Morphometry of Closed, Implicit Surfaces

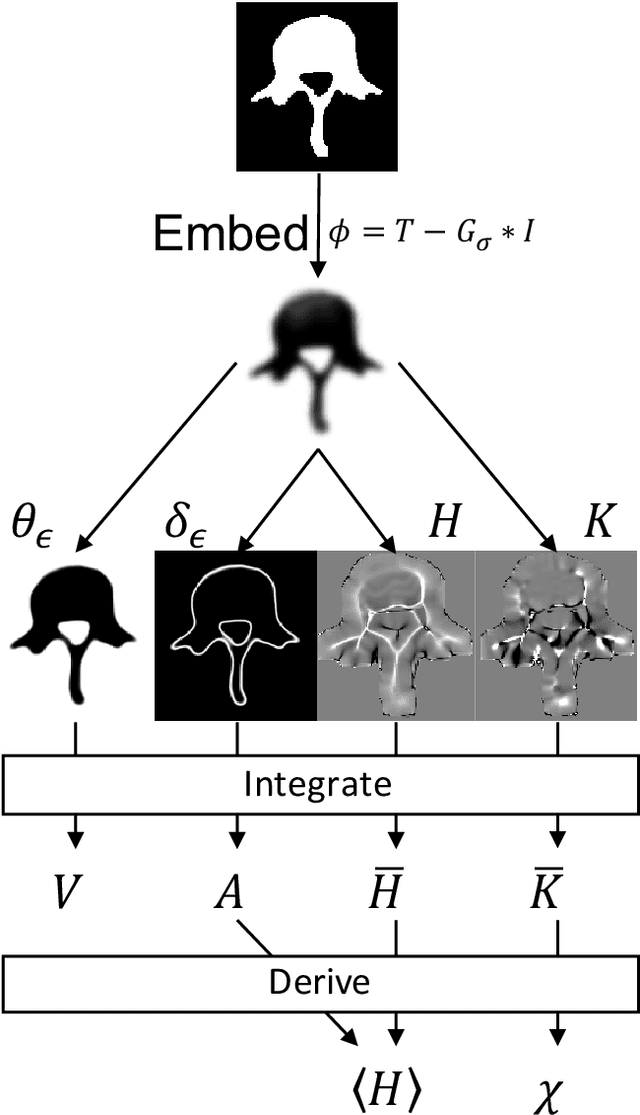
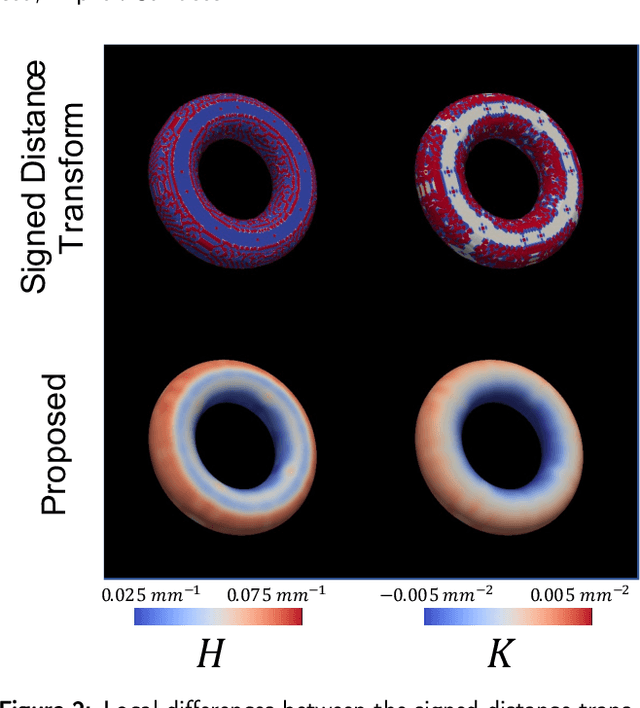
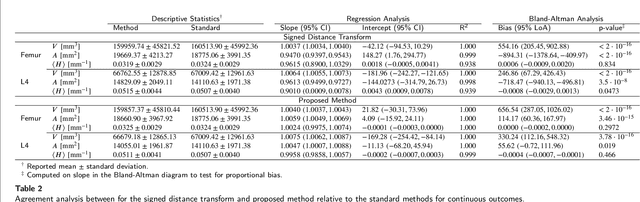
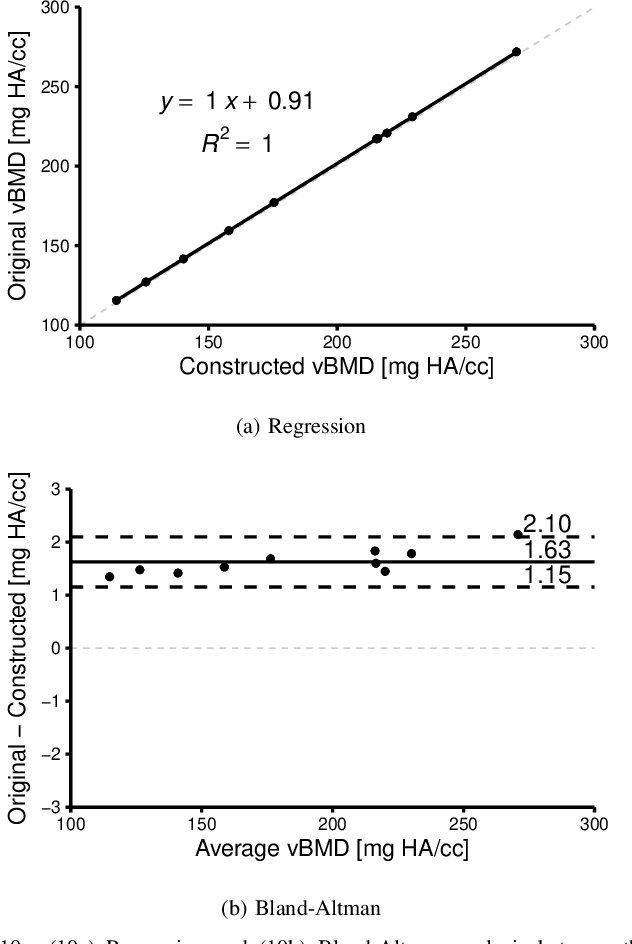
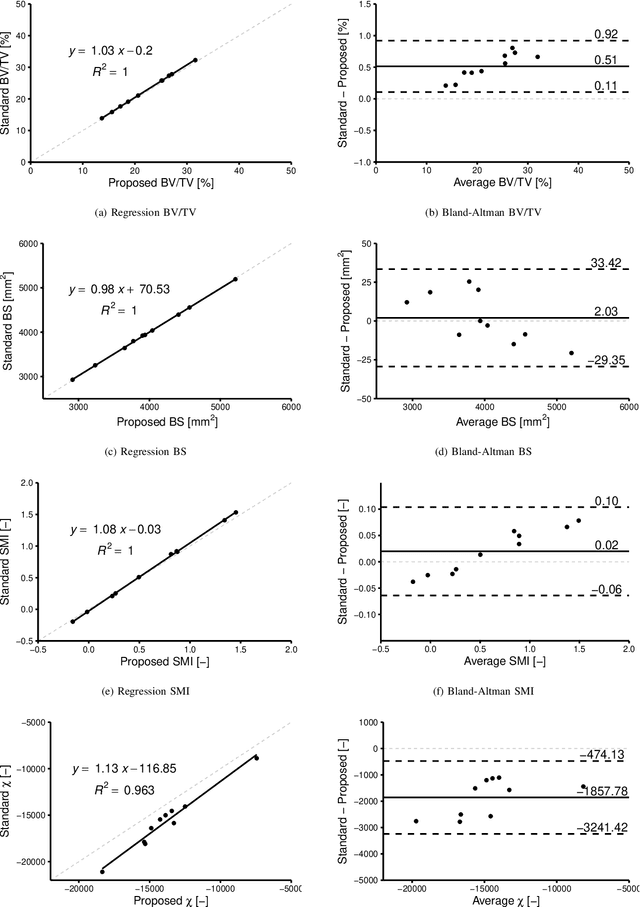
Anatomical structures such as the hippocampus, liver, and bones can be analyzed as orientable, closed surfaces. This permits the computation of volume, surface area, mean curvature, Gaussian curvature, and the Euler-Poincar\'e characteristic as well as comparison of these morphometrics between structures of different topology. The structures are commonly represented implicitly in curve evolution problems as the zero level set of an embedding. Practically, binary images of anatomical structures are embedded using a signed distance transform. However, quantization prevents the accurate computation of curvatures, leading to considerable errors in morphometry. This paper presents a fast, simple embedding procedure for accurate local morphometry as the zero crossing of the Gaussian blurred binary image. The proposed method was validated based on the femur and fourth lumbar vertebrae of 50 clinical computed tomography datasets. The results show that the signed distance transform leads to large quantization errors in the computed local curvature. Global validation of morphometry using regression and Bland-Altman analysis revealed that the coefficient of determination for the average mean curvature is improved from 93.8% with the signed distance transform to 100% with the proposed method. For the surface area, the proportional bias is improved from -5.0% for the signed distance transform to +0.6% for the proposed method. The Euler-Poincar\'e characteristic is improved from unusable in the signed distance transform to 98% accuracy for the proposed method. The proposed method enables an improved local and global evaluation of curvature for purposes of morphometry on closed, implicit surfaces.

Robust Self-Supervised Learning of Deterministic Errors in Single-Plane (Monoplanar) and Dual-Plane (Biplanar) X-ray Fluoroscopy

Fluoroscopic imaging that captures X-ray images at video framerates is advantageous for guiding catheter insertions by vascular surgeons and interventional radiologists. Visualizing the dynamical movements non-invasively allows complex surgical procedures to be performed with less trauma to the patient. To improve surgical precision, endovascular procedures can benefit from more accurate fluoroscopy data via calibration. This paper presents a robust self-calibration algorithm suitable for single-plane and dual-plane fluoroscopy. A three-dimensional (3D) target field was imaged by the fluoroscope in a strong geometric network configuration. The unknown 3D positions of targets and the fluoroscope pose were estimated simultaneously by maximizing the likelihood of the Student-t probability distribution function. A smoothed k-nearest neighbour (kNN) regression is then used to model the deterministic component of the image reprojection error of the robust bundle adjustment. The Maximum Likelihood Estimation step and the kNN regression step are then repeated iteratively until convergence. Four different error modeling schemes were compared while varying the quantity of training images. It was found that using a smoothed kNN regression can automatically model the systematic errors in fluoroscopy with similar accuracy as a human expert using a small training dataset. When all training images were used, the 3D mapping error was reduced from 0.61-0.83 mm to 0.04 mm post-calibration (94.2-95.7% improvement), and the 2D reprojection error was reduced from 1.17-1.31 to 0.20-0.21 pixels (83.2-83.8% improvement). When using biplanar fluoroscopy, the 3D measurement accuracy of the system improved from 0.60 mm to 0.32 mm (47.2% improvement).