High-Order Signed Distance Transform of Sampled Signals
Paper and Code
Oct 26, 2021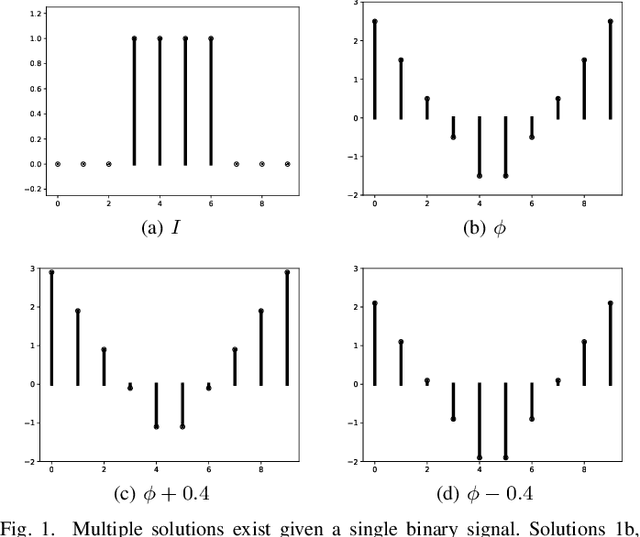

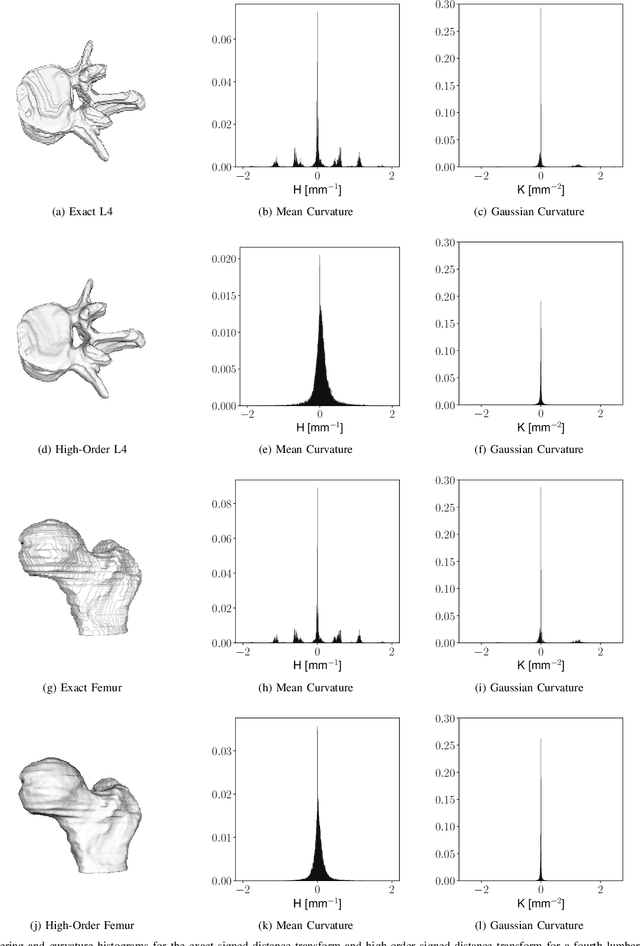
Signed distance transforms of sampled signals can be constructed better than the traditional exact signed distance transform. Such a transform is termed the high-order signed distance transform and is defined as satisfying three conditions: the Eikonal equation, recovery by a Heaviside function, and has an order of accuracy greater than unity away from the medial axis. Such a transform is an improvement to the classic notion of an exact signed distance transform because it does not exhibit artifacts of quantization. A large constant, linear time complexity high-order signed distance transform for arbitrary dimensionality sampled signals is developed based on the high order fast sweeping method. The transform is initialized with an exact signed distance transform and quantization corrected through an upwind solver for the boundary value Eikonal equation. The proposed method cannot attain arbitrary order of accuracy and is limited by the initialization method and non-uniqueness of the problem. However, meshed surfaces are visually smoother and do not exhibit artifacts of quantization in local mean and Gaussian curvature.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge