Constructing High-Order Signed Distance Maps from Computed Tomography Data with Application to Bone Morphometry

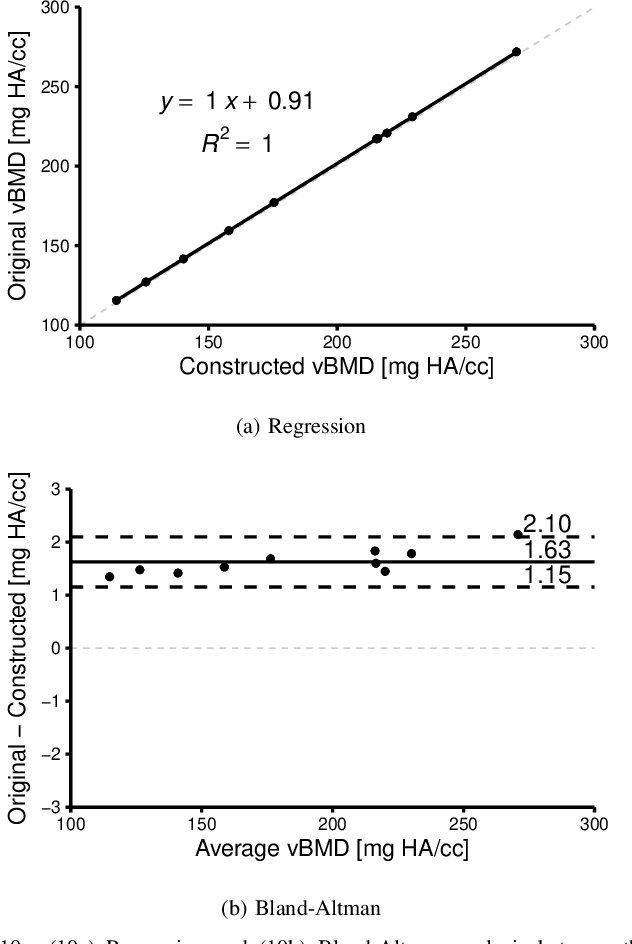
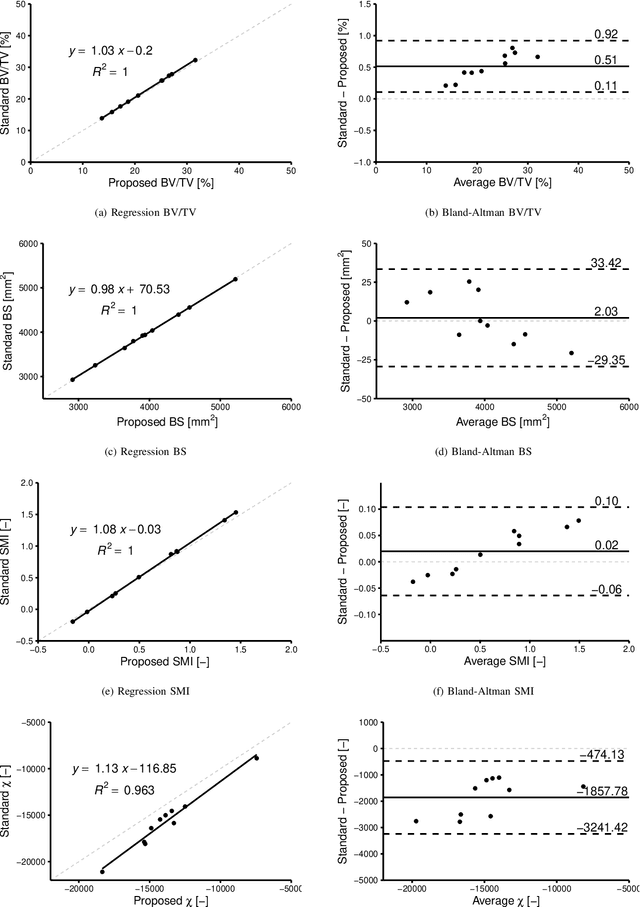
An algorithm is presented for constructing high-order signed distance fields for two phase materials imaged with computed tomography. The signed distance field is high-order in that it is free of the quantization artifact associated with the distance transform of sampled signals. The narrowband is solved using a closest point algorithm extended for implicit embeddings that are not a signed distance field. The high-order fast sweeping algorithm is used to extend the narrowband to the remainder of the domain. The order of accuracy of the narrowband and extension methods are verified on ideal implicit surfaces. The method is applied to ten excised cubes of bovine trabecular bone. Localization of the surface, estimation of phase densities, and local morphometry is validated with these subjects. Since the embedding is high-order, gradients and thus curvatures can be accurately estimated locally in the image data.

High-Order Signed Distance Transform of Sampled Signals

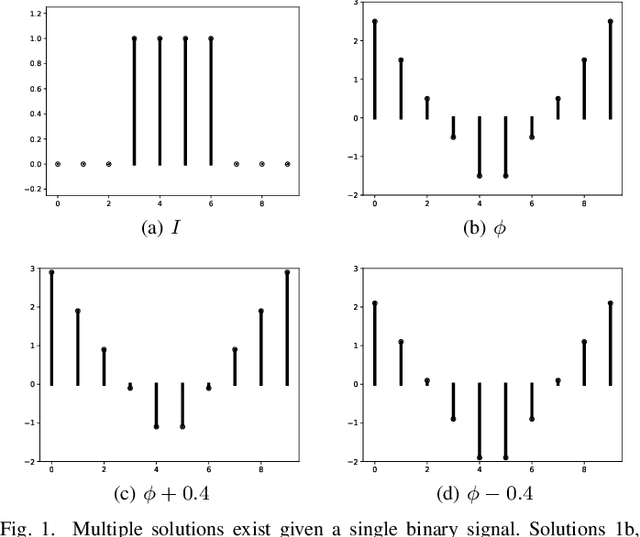
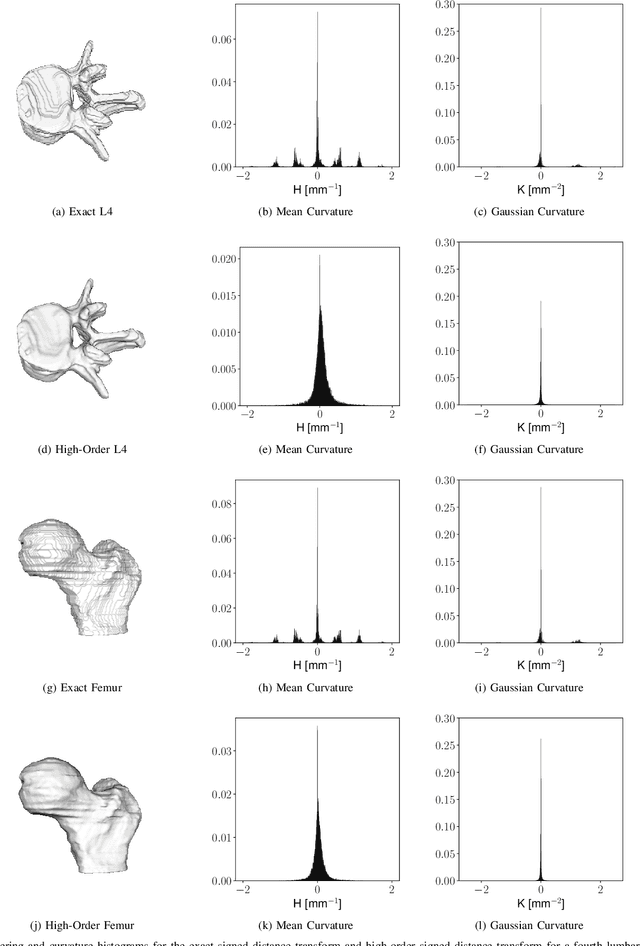
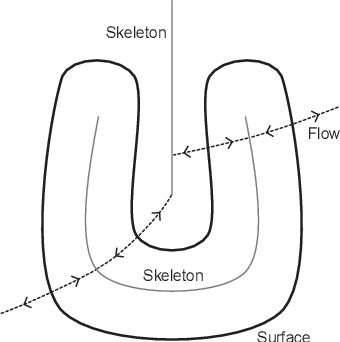
Signed distance transforms of sampled signals can be constructed better than the traditional exact signed distance transform. Such a transform is termed the high-order signed distance transform and is defined as satisfying three conditions: the Eikonal equation, recovery by a Heaviside function, and has an order of accuracy greater than unity away from the medial axis. Such a transform is an improvement to the classic notion of an exact signed distance transform because it does not exhibit artifacts of quantization. A large constant, linear time complexity high-order signed distance transform for arbitrary dimensionality sampled signals is developed based on the high order fast sweeping method. The transform is initialized with an exact signed distance transform and quantization corrected through an upwind solver for the boundary value Eikonal equation. The proposed method cannot attain arbitrary order of accuracy and is limited by the initialization method and non-uniqueness of the problem. However, meshed surfaces are visually smoother and do not exhibit artifacts of quantization in local mean and Gaussian curvature.