Andrew S. Michalski
Local Morphometry of Closed, Implicit Surfaces
Jul 29, 2021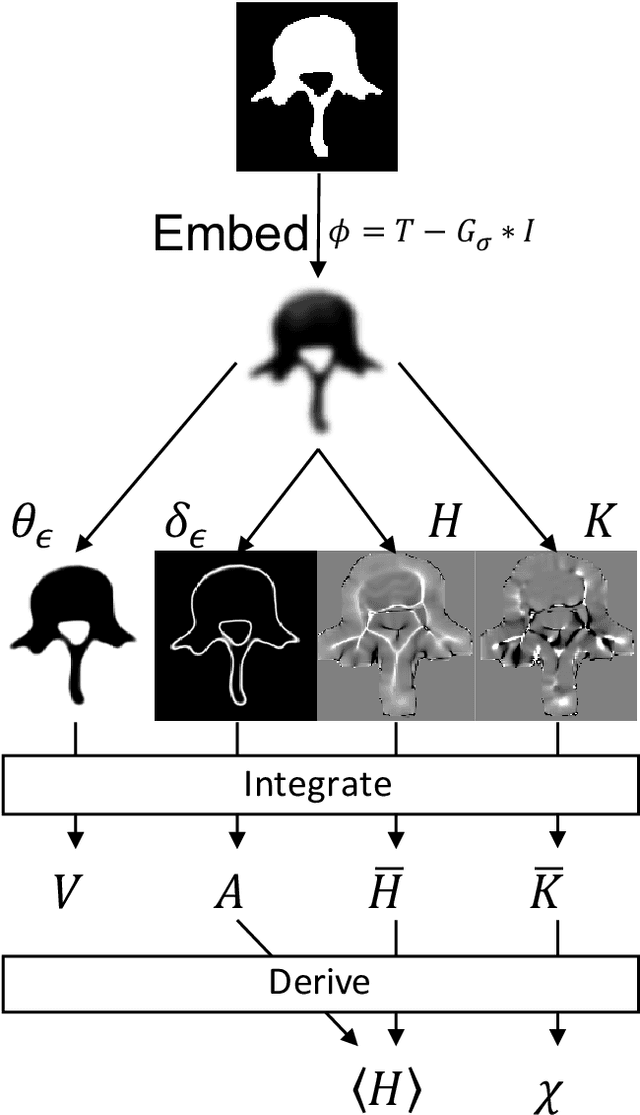
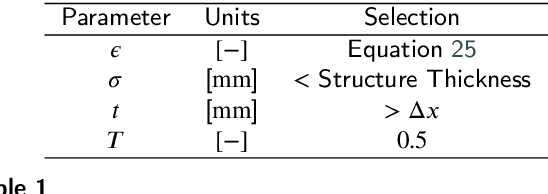
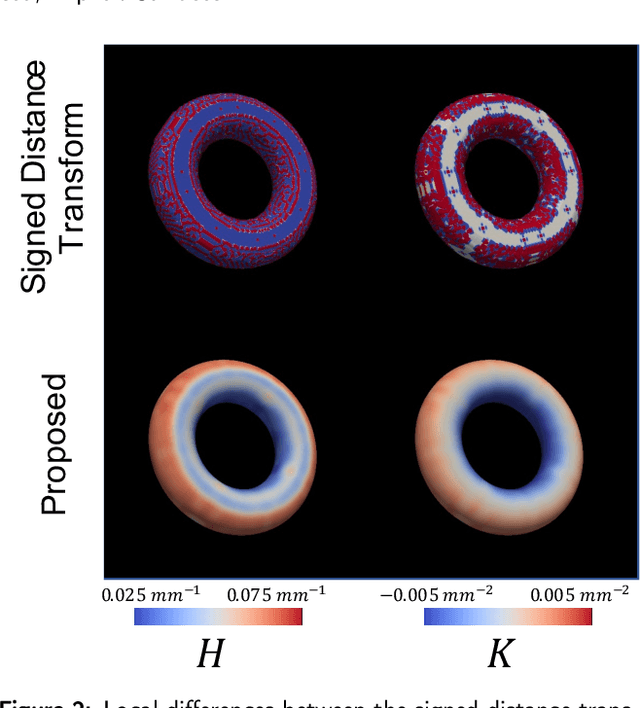
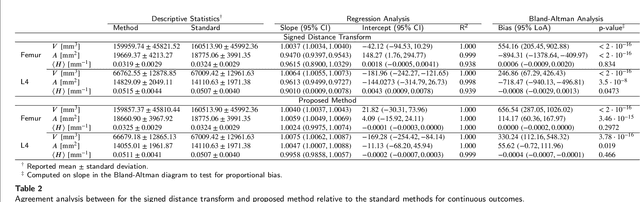
Abstract:Anatomical structures such as the hippocampus, liver, and bones can be analyzed as orientable, closed surfaces. This permits the computation of volume, surface area, mean curvature, Gaussian curvature, and the Euler-Poincar\'e characteristic as well as comparison of these morphometrics between structures of different topology. The structures are commonly represented implicitly in curve evolution problems as the zero level set of an embedding. Practically, binary images of anatomical structures are embedded using a signed distance transform. However, quantization prevents the accurate computation of curvatures, leading to considerable errors in morphometry. This paper presents a fast, simple embedding procedure for accurate local morphometry as the zero crossing of the Gaussian blurred binary image. The proposed method was validated based on the femur and fourth lumbar vertebrae of 50 clinical computed tomography datasets. The results show that the signed distance transform leads to large quantization errors in the computed local curvature. Global validation of morphometry using regression and Bland-Altman analysis revealed that the coefficient of determination for the average mean curvature is improved from 93.8% with the signed distance transform to 100% with the proposed method. For the surface area, the proportional bias is improved from -5.0% for the signed distance transform to +0.6% for the proposed method. The Euler-Poincar\'e characteristic is improved from unusable in the signed distance transform to 98% accuracy for the proposed method. The proposed method enables an improved local and global evaluation of curvature for purposes of morphometry on closed, implicit surfaces.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge