Assessing the risk of re-identification arising from an attack on anonymised data

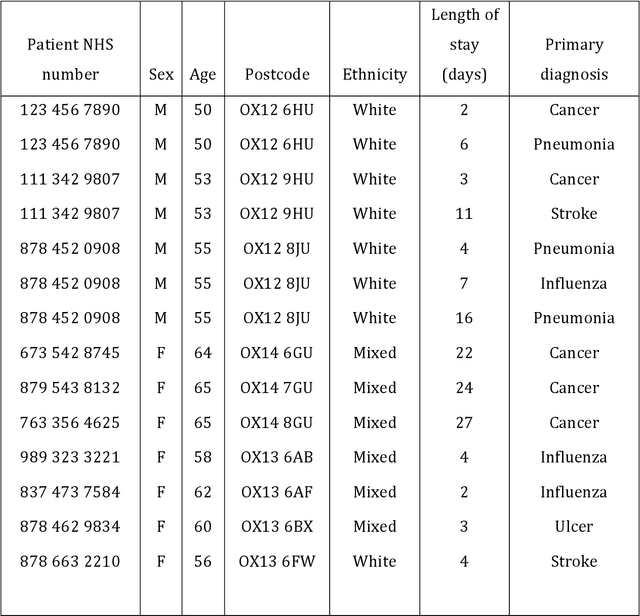
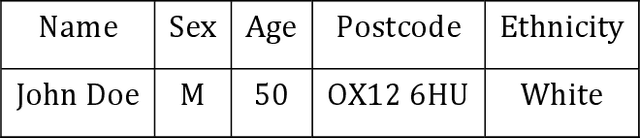
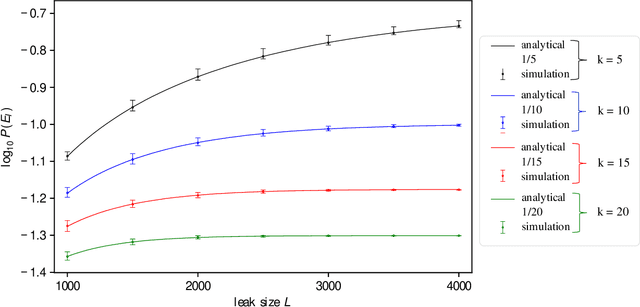
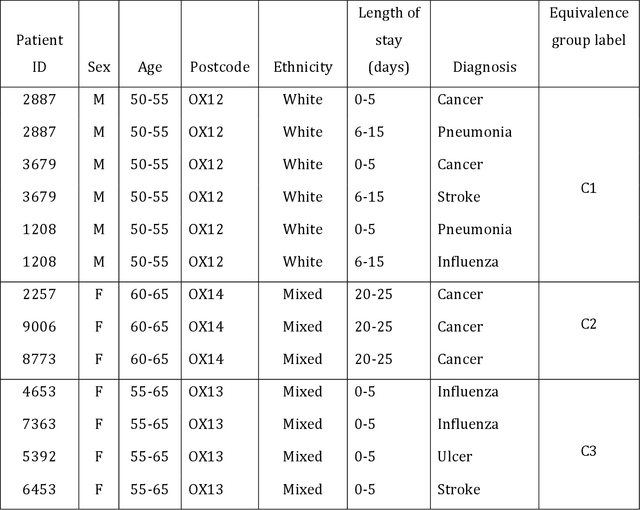
Objective: The use of routinely-acquired medical data for research purposes requires the protection of patient confidentiality via data anonymisation. The objective of this work is to calculate the risk of re-identification arising from a malicious attack to an anonymised dataset, as described below. Methods: We first present an analytical means of estimating the probability of re-identification of a single patient in a k-anonymised dataset of Electronic Health Record (EHR) data. Second, we generalize this solution to obtain the probability of multiple patients being re-identified. We provide synthetic validation via Monte Carlo simulations to illustrate the accuracy of the estimates obtained. Results: The proposed analytical framework for risk estimation provides re-identification probabilities that are in agreement with those provided by simulation in a number of scenarios. Our work is limited by conservative assumptions which inflate the re-identification probability. Discussion: Our estimates show that the re-identification probability increases with the proportion of the dataset maliciously obtained and that it has an inverse relationship with the equivalence class size. Our recursive approach extends the applicability domain to the general case of a multi-patient re-identification attack in an arbitrary k-anonymisation scheme. Conclusion: We prescribe a systematic way to parametrize the k-anonymisation process based on a pre-determined re-identification probability. We observed that the benefits of a reduced re-identification risk that come with increasing k-size may not be worth the reduction in data granularity when one is considering benchmarking the re-identification probability on the size of the portion of the dataset maliciously obtained by the adversary.

Offline bilingual word vectors, orthogonal transformations and the inverted softmax

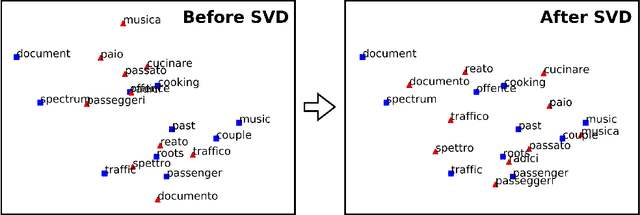
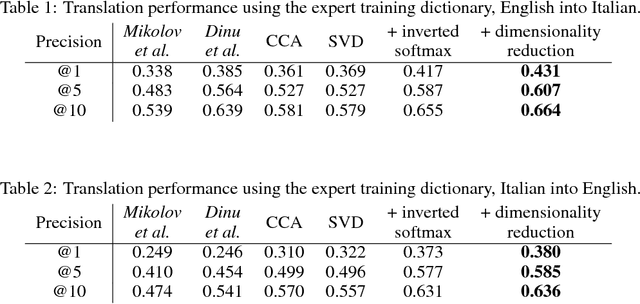
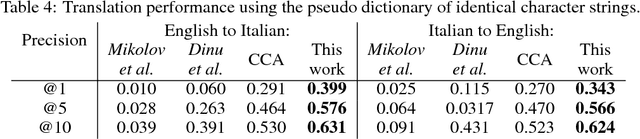
Usually bilingual word vectors are trained "online". Mikolov et al. showed they can also be found "offline", whereby two pre-trained embeddings are aligned with a linear transformation, using dictionaries compiled from expert knowledge. In this work, we prove that the linear transformation between two spaces should be orthogonal. This transformation can be obtained using the singular value decomposition. We introduce a novel "inverted softmax" for identifying translation pairs, with which we improve the precision @1 of Mikolov's original mapping from 34% to 43%, when translating a test set composed of both common and rare English words into Italian. Orthogonal transformations are more robust to noise, enabling us to learn the transformation without expert bilingual signal by constructing a "pseudo-dictionary" from the identical character strings which appear in both languages, achieving 40% precision on the same test set. Finally, we extend our method to retrieve the true translations of English sentences from a corpus of 200k Italian sentences with a precision @1 of 68%.

Sorting out symptoms: design and evaluation of the 'babylon check' automated triage system

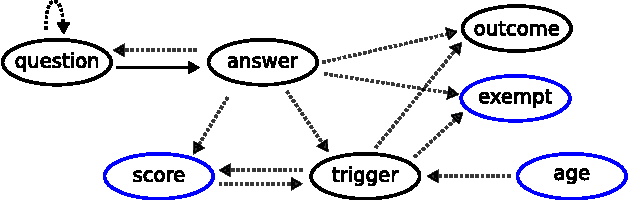
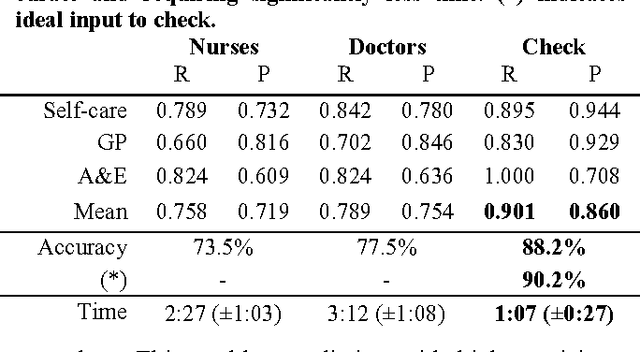
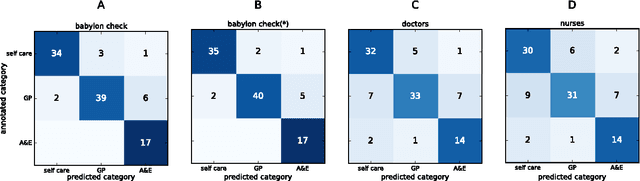
Prior to seeking professional medical care it is increasingly common for patients to use online resources such as automated symptom checkers. Many such systems attempt to provide a differential diagnosis based on the symptoms elucidated from the user, which may lead to anxiety if life or limb-threatening conditions are part of the list, a phenomenon termed 'cyberchondria' [1]. Systems that provide advice on where to seek help, rather than a diagnosis, are equally popular, and in our view provide the most useful information. In this technical report we describe how such a triage system can be modelled computationally, how medical insights can be translated into triage flows, and how such systems can be validated and tested. We present babylon check, our commercially deployed automated triage system, as a case study, and illustrate its performance in a large, semi-naturalistic deployment study.