3D Target Detection and Spectral Classification for Single-photon LiDAR Data

3D single-photon LiDAR imaging has an important role in many applications. However, full deployment of this modality will require the analysis of low signal to noise ratio target returns and a very high volume of data. This is particularly evident when imaging through obscurants or in high ambient background light conditions. This paper proposes a multiscale approach for 3D surface detection from the photon timing histogram to permit a significant reduction in data volume. The resulting surfaces are background-free and can be used to infer depth and reflectivity information about the target. We demonstrate this by proposing a hierarchical Bayesian model for 3D reconstruction and spectral classification of multispectral single-photon LiDAR data. The reconstruction method promotes spatial correlation between point-cloud estimates and uses a coordinate gradient descent algorithm for parameter estimation. Results on simulated and real data show the benefits of the proposed target detection and reconstruction approaches when compared to state-of-the-art processing algorithms

Sparse Linear Spectral Unmixing of Hyperspectral images using Expectation-Propagation

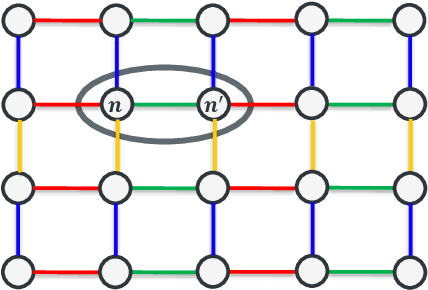
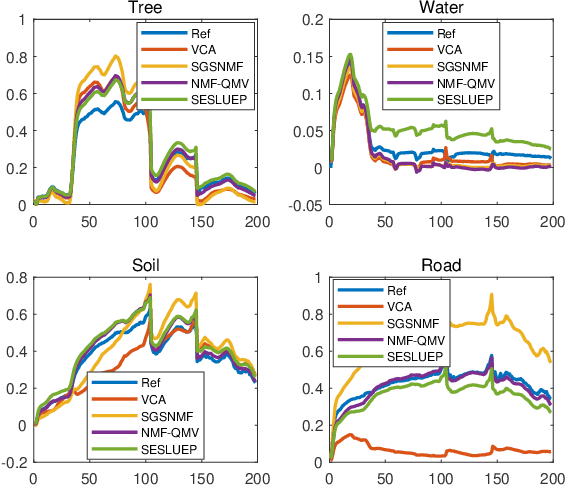
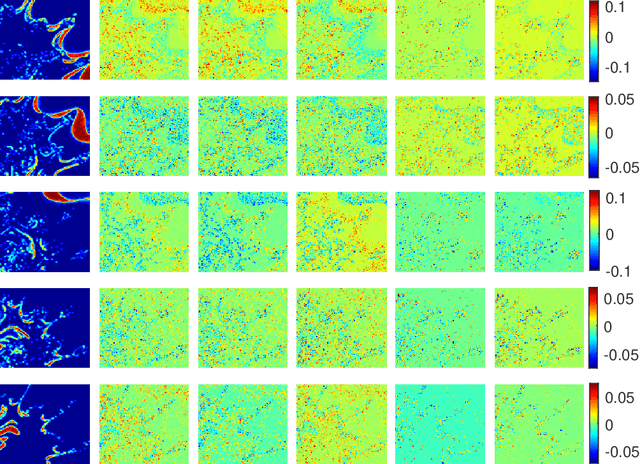
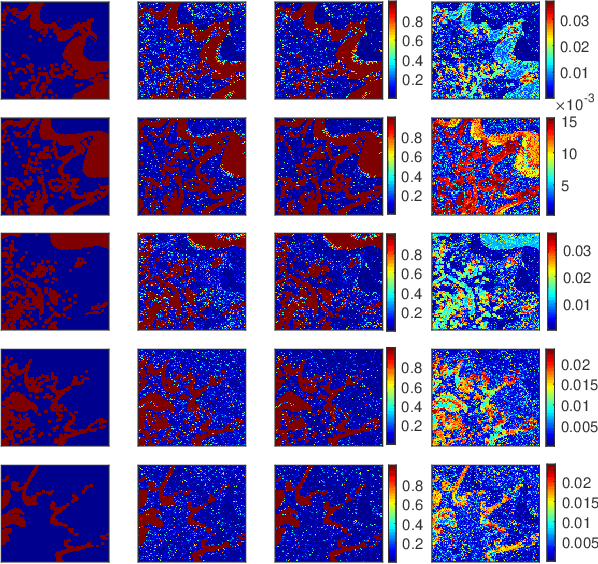
This paper presents a novel Bayesian approach for hyperspectral image unmixing. The observed pixels are modeled by a linear combination of material signatures weighted by their corresponding abundances. A spike-and-slab abundance prior is adopted to promote sparse mixtures and an Ising prior model is used to capture spatial correlation of the mixture support across pixels. We approximate the posterior distribution of the abundances using the expectation-propagation (EP) method. We show that it can significantly reduce the computational complexity of the unmixing stage and meanwhile provide uncertainty measures, compared to expensive Monte Carlo strategies traditionally considered for uncertainty quantification. Moreover, many variational parameters within each EP factor can be updated in a parallel manner, which enables mapping of efficient algorithmic architectures based on graphics processing units (GPU). Under the same approximate Bayesian framework, we then extend the proposed algorithm to semi-supervised unmixing, whereby the abundances are viewed as latent variables and the expectation-maximization (EM) algorithm is used to refine the endmember matrix. Experimental results on synthetic data and real hyperspectral data illustrate the benefits of the proposed framework over state-of-art linear unmixing methods.