Stephen Chu
A constrained clustering based approach for matching a collection of feature sets
Jun 12, 2016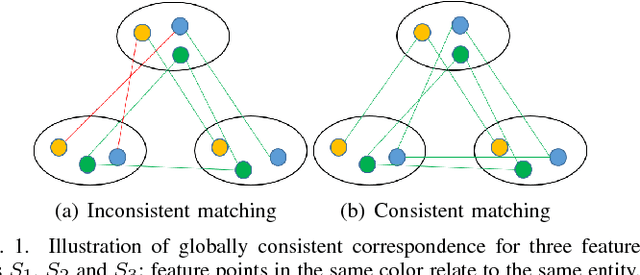
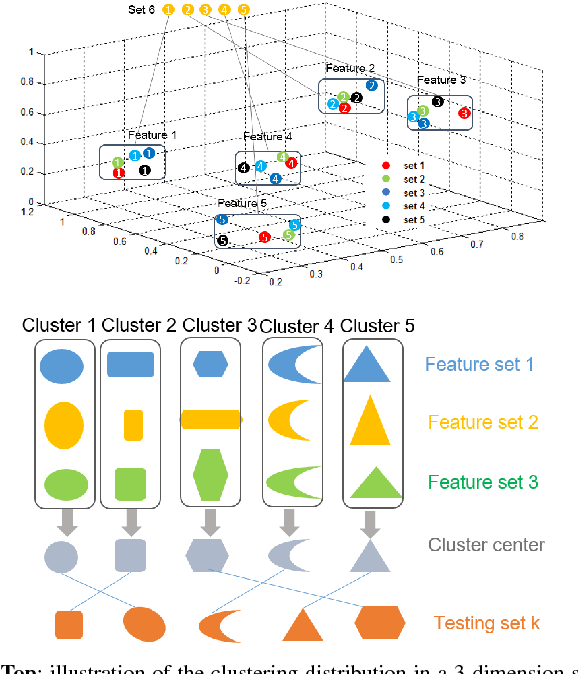
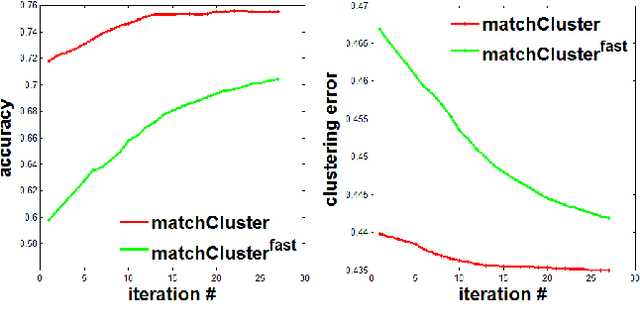
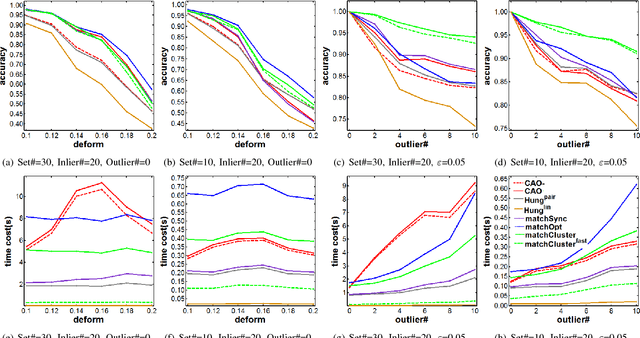
Abstract:In this paper, we consider the problem of finding the feature correspondences among a collection of feature sets, by using their point-wise unary features. This is a fundamental problem in computer vision and pattern recognition, which also closely relates to other areas such as operational research. Different from two-set matching which can be transformed to a quadratic assignment programming task that is known NP-hard, inclusion of merely unary attributes leads to a linear assignment problem for matching two feature sets. This problem has been well studied and there are effective polynomial global optimum solvers such as the Hungarian method. However, it becomes ill-posed when the unary attributes are (heavily) corrupted. The global optimal correspondence concerning the best score defined by the attribute affinity/cost between the two sets can be distinct to the ground truth correspondence since the score function is biased by noises. To combat this issue, we devise a method for matching a collection of feature sets by synergetically exploring the information across the sets. In general, our method can be perceived from a (constrained) clustering perspective: in each iteration, it assigns the features of one set to the clusters formed by the rest of feature sets, and updates the cluster centers in turn. Results on both synthetic data and real images suggest the efficacy of our method against state-of-the-arts.
A General Multi-Graph Matching Approach via Graduated Consistency-regularized Boosting
Feb 20, 2015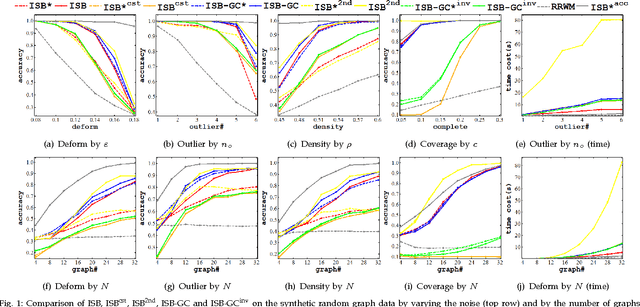

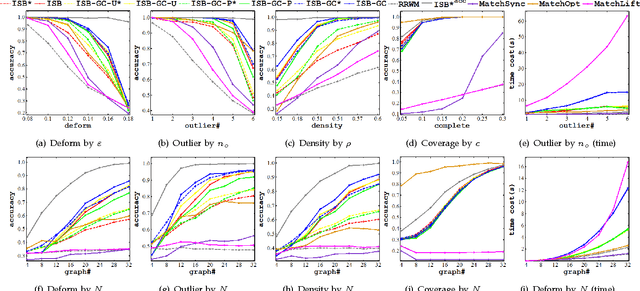
Abstract:This paper addresses the problem of matching $N$ weighted graphs referring to an identical object or category. More specifically, matching the common node correspondences among graphs. This multi-graph matching problem involves two ingredients affecting the overall accuracy: i) the local pairwise matching affinity score among graphs; ii) the global matching consistency that measures the uniqueness of the pairwise matching results by different chaining orders. Previous studies typically either enforce the matching consistency constraints in the beginning of iterative optimization, which may propagate matching error both over iterations and across graph pairs; or separate affinity optimizing and consistency regularization in two steps. This paper is motivated by the observation that matching consistency can serve as a regularizer in the affinity objective function when the function is biased due to noises or inappropriate modeling. We propose multi-graph matching methods to incorporate the two aspects by boosting the affinity score, meanwhile gradually infusing the consistency as a regularizer. Furthermore, we propose a node-wise consistency/affinity-driven mechanism to elicit the common inlier nodes out of the irrelevant outliers. Extensive results on both synthetic and public image datasets demonstrate the competency of the proposed algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge