A General Multi-Graph Matching Approach via Graduated Consistency-regularized Boosting
Paper and Code
Feb 20, 2015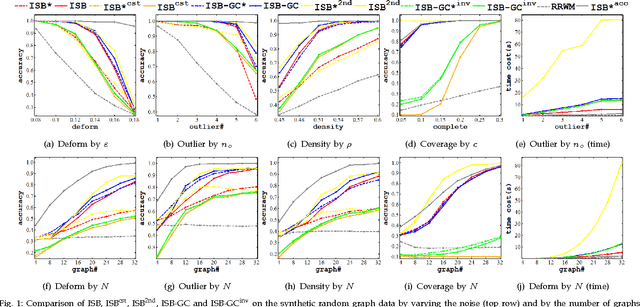

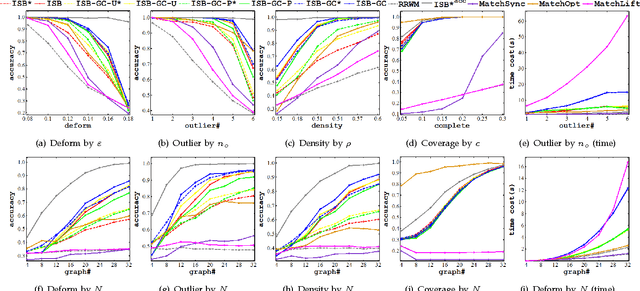
This paper addresses the problem of matching $N$ weighted graphs referring to an identical object or category. More specifically, matching the common node correspondences among graphs. This multi-graph matching problem involves two ingredients affecting the overall accuracy: i) the local pairwise matching affinity score among graphs; ii) the global matching consistency that measures the uniqueness of the pairwise matching results by different chaining orders. Previous studies typically either enforce the matching consistency constraints in the beginning of iterative optimization, which may propagate matching error both over iterations and across graph pairs; or separate affinity optimizing and consistency regularization in two steps. This paper is motivated by the observation that matching consistency can serve as a regularizer in the affinity objective function when the function is biased due to noises or inappropriate modeling. We propose multi-graph matching methods to incorporate the two aspects by boosting the affinity score, meanwhile gradually infusing the consistency as a regularizer. Furthermore, we propose a node-wise consistency/affinity-driven mechanism to elicit the common inlier nodes out of the irrelevant outliers. Extensive results on both synthetic and public image datasets demonstrate the competency of the proposed algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge