A constrained clustering based approach for matching a collection of feature sets
Paper and Code
Jun 12, 2016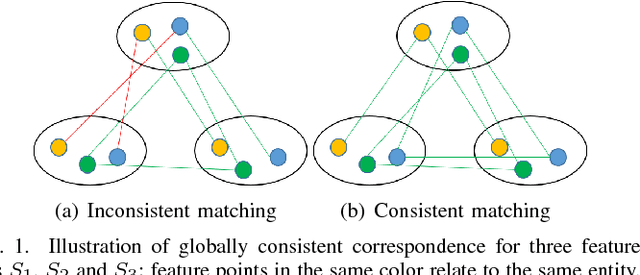
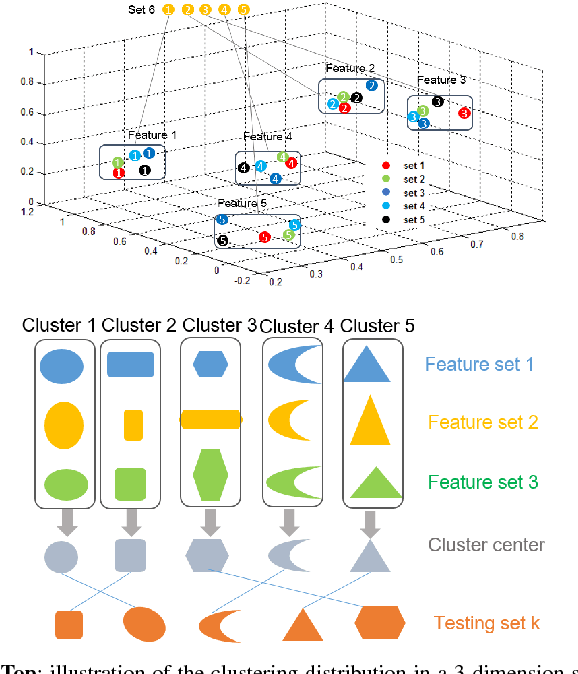
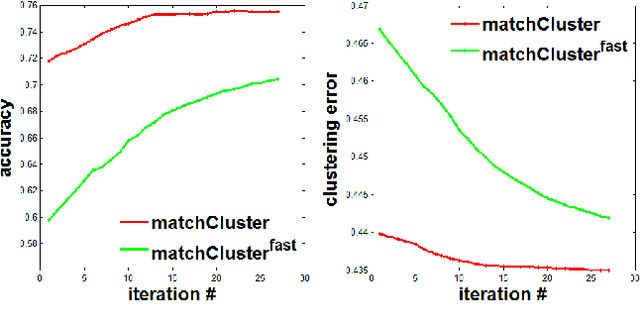
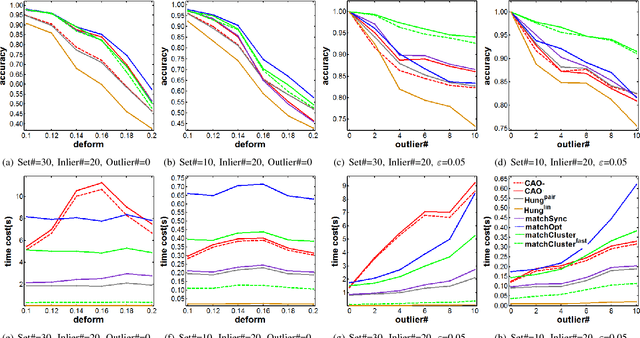
In this paper, we consider the problem of finding the feature correspondences among a collection of feature sets, by using their point-wise unary features. This is a fundamental problem in computer vision and pattern recognition, which also closely relates to other areas such as operational research. Different from two-set matching which can be transformed to a quadratic assignment programming task that is known NP-hard, inclusion of merely unary attributes leads to a linear assignment problem for matching two feature sets. This problem has been well studied and there are effective polynomial global optimum solvers such as the Hungarian method. However, it becomes ill-posed when the unary attributes are (heavily) corrupted. The global optimal correspondence concerning the best score defined by the attribute affinity/cost between the two sets can be distinct to the ground truth correspondence since the score function is biased by noises. To combat this issue, we devise a method for matching a collection of feature sets by synergetically exploring the information across the sets. In general, our method can be perceived from a (constrained) clustering perspective: in each iteration, it assigns the features of one set to the clusters formed by the rest of feature sets, and updates the cluster centers in turn. Results on both synthetic data and real images suggest the efficacy of our method against state-of-the-arts.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge