When are LLMs Sufficient Policy Optimizers for Sequential RL Tasks?

We study when large language models (LLMs) can serve as effective black-box policy optimizers for reinforcement learning (RL) tasks, i.e., when can we replace classical RL algorithms with an LLM? We explore this question by introducing Prompted Policy Optimization (PromptPO), an iterative method that prompts an LLM with Python descriptions of the state space, action space, and reward function, then has it generate and refine executable policies based on rollout feedback. Across hard exploration environments, Meta-World robotics tasks, and several real-world control problems, PromptPO often matches or exceeds the performance of standard RL baselines while using substantially fewer environment interactions. To maximize expected return, and without further explicit prompting, the policies PromptPO outputs range from tuned proportional controllers or rule-based plans to policies that run planning algorithms like value iteration. Our results demonstrate that LLM-based policy optimization is sufficient when the LLM can leverage prior knowledge about the environment or optimization strategy. PromptPO underperforms standard RL baselines in MuJoCo domains. This demonstrates possible limitations of LLM-based policy optimization to settings that requiring fine-grained continuous control.

Influencing Humans to Conform to Preference Models for RLHF

Designing a reinforcement learning from human feedback (RLHF) algorithm to approximate a human's unobservable reward function requires assuming, implicitly or explicitly, a model of human preferences. A preference model that poorly describes how humans generate preferences risks learning a poor approximation of the human's reward function. In this paper, we conduct three human studies to asses whether one can influence the expression of real human preferences to more closely conform to a desired preference model. Importantly, our approach does not seek to alter the human's unobserved reward function. Rather, we change how humans use this reward function to generate preferences, such that they better match whatever preference model is assumed by a particular RLHF algorithm. We introduce three interventions: showing humans the quantities that underlie a preference model, which is normally unobservable information derived from the reward function; training people to follow a specific preference model; and modifying the preference elicitation question. All intervention types show significant effects, providing practical tools to improve preference data quality and the resultant alignment of the learned reward functions. Overall we establish a novel research direction in model alignment: designing interfaces and training interventions to increase human conformance with the modeling assumptions of the algorithm that will learn from their input.

Learning Optimal Advantage from Preferences and Mistaking it for Reward

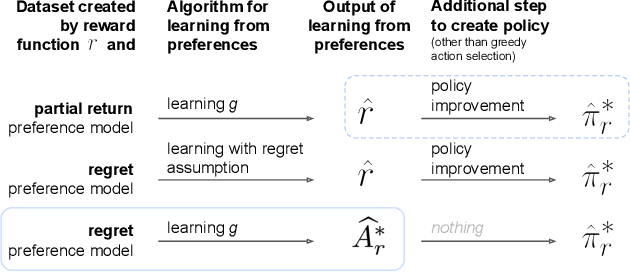
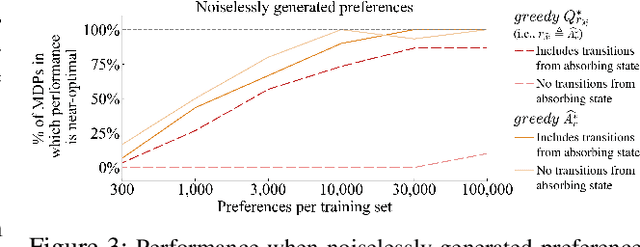
We consider algorithms for learning reward functions from human preferences over pairs of trajectory segments, as used in reinforcement learning from human feedback (RLHF). Most recent work assumes that human preferences are generated based only upon the reward accrued within those segments, or their partial return. Recent work casts doubt on the validity of this assumption, proposing an alternative preference model based upon regret. We investigate the consequences of assuming preferences are based upon partial return when they actually arise from regret. We argue that the learned function is an approximation of the optimal advantage function, $\hat{A^*_r}$, not a reward function. We find that if a specific pitfall is addressed, this incorrect assumption is not particularly harmful, resulting in a highly shaped reward function. Nonetheless, this incorrect usage of $\hat{A^*_r}$ is less desirable than the appropriate and simpler approach of greedy maximization of $\hat{A^*_r}$. From the perspective of the regret preference model, we also provide a clearer interpretation of fine tuning contemporary large language models with RLHF. This paper overall provides insight regarding why learning under the partial return preference model tends to work so well in practice, despite it conforming poorly to how humans give preferences.

Models of human preference for learning reward functions

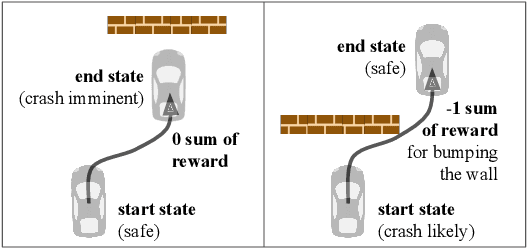
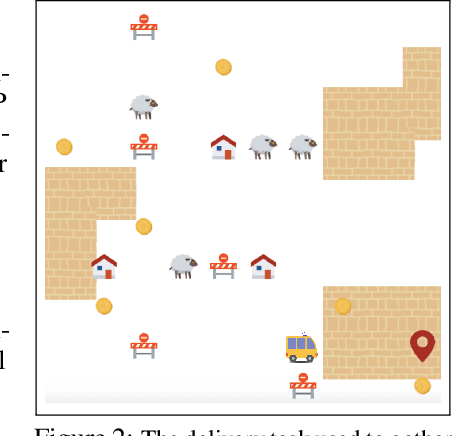
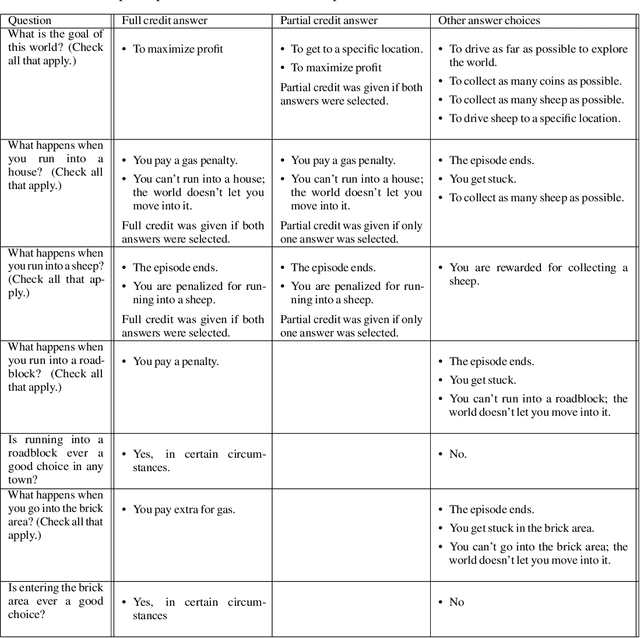
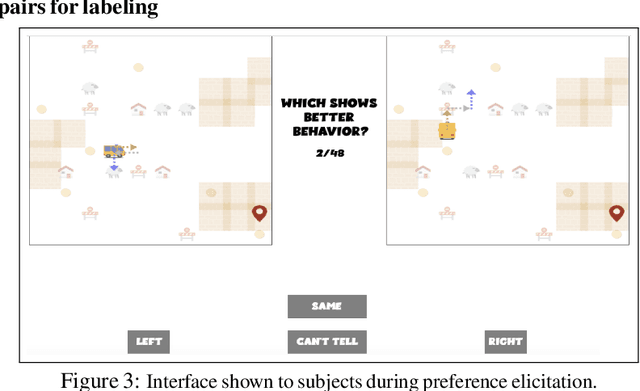
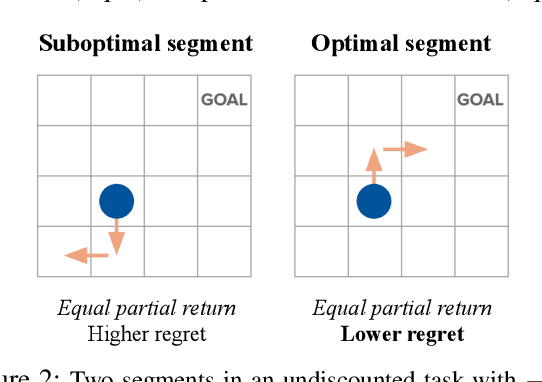
The utility of reinforcement learning is limited by the alignment of reward functions with the interests of human stakeholders. One promising method for alignment is to learn the reward function from human-generated preferences between pairs of trajectory segments. These human preferences are typically assumed to be informed solely by partial return, the sum of rewards along each segment. We find this assumption to be flawed and propose modeling preferences instead as arising from a different statistic: each segment's regret, a measure of a segment's deviation from optimal decision-making. Given infinitely many preferences generated according to regret, we prove that we can identify a reward function equivalent to the reward function that generated those preferences. We also prove that the previous partial return model lacks this identifiability property without preference noise that reveals rewards' relative proportions, and we empirically show that our proposed regret preference model outperforms it with finite training data in otherwise the same setting. Additionally, our proposed regret preference model better predicts real human preferences and also learns reward functions from these preferences that lead to policies that are better human-aligned. Overall, this work establishes that the choice of preference model is impactful, and our proposed regret preference model provides an improvement upon a core assumption of recent research.