Learning Optimal Advantage from Preferences and Mistaking it for Reward

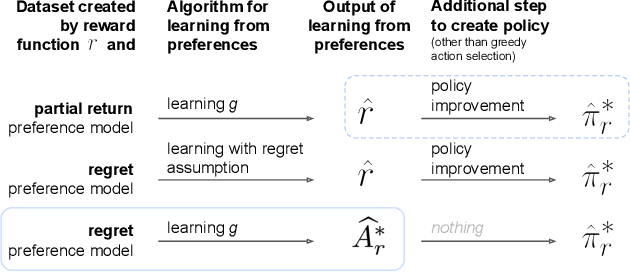
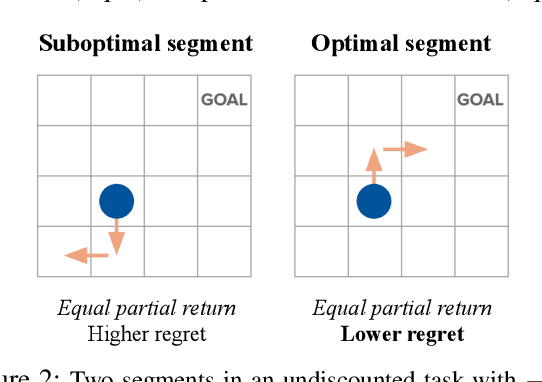
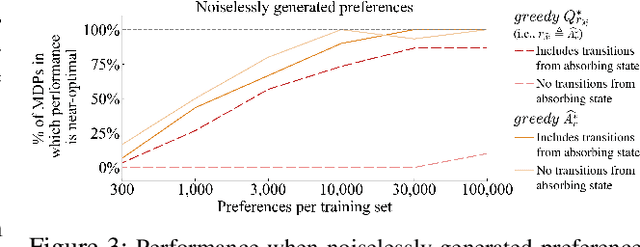
We consider algorithms for learning reward functions from human preferences over pairs of trajectory segments, as used in reinforcement learning from human feedback (RLHF). Most recent work assumes that human preferences are generated based only upon the reward accrued within those segments, or their partial return. Recent work casts doubt on the validity of this assumption, proposing an alternative preference model based upon regret. We investigate the consequences of assuming preferences are based upon partial return when they actually arise from regret. We argue that the learned function is an approximation of the optimal advantage function, $\hat{A^*_r}$, not a reward function. We find that if a specific pitfall is addressed, this incorrect assumption is not particularly harmful, resulting in a highly shaped reward function. Nonetheless, this incorrect usage of $\hat{A^*_r}$ is less desirable than the appropriate and simpler approach of greedy maximization of $\hat{A^*_r}$. From the perspective of the regret preference model, we also provide a clearer interpretation of fine tuning contemporary large language models with RLHF. This paper overall provides insight regarding why learning under the partial return preference model tends to work so well in practice, despite it conforming poorly to how humans give preferences.

B$^3$RTDP: A Belief Branch and Bound Real-Time Dynamic Programming Approach to Solving POMDPs

Partially Observable Markov Decision Processes (POMDPs) offer a promising world representation for autonomous agents, as they can model both transitional and perceptual uncertainties. Calculating the optimal solution to POMDP problems can be computationally expensive as they require reasoning over the (possibly infinite) space of beliefs. Several approaches have been proposed to overcome this difficulty, such as discretizing the belief space, point-based belief sampling, and Monte Carlo tree search. The Real-Time Dynamic Programming approach of the RTDP-Bel algorithm approximates the value function by storing it in a hashtable with discretized belief keys. We propose an extension to the RTDP-Bel algorithm which we call Belief Branch and Bound RTDP (B$^3$RTDP). Our algorithm uses a bounded value function representation and takes advantage of this in two novel ways: a search-bounding technique based on action selection convergence probabilities, and a method for leveraging early action convergence called the \textit{Convergence Frontier}. Lastly, we empirically demonstrate that B$^3$RTDP can achieve greater returns in less time than the state-of-the-art SARSOP solver on known POMDP problems.