Reverse Probing: Evaluating Knowledge Transfer via Finetuned Task Embeddings for Coreference Resolution

In this work, we reimagine classical probing to evaluate knowledge transfer from simple source to more complex target tasks. Instead of probing frozen representations from a complex source task on diverse simple target probing tasks (as usually done in probing), we explore the effectiveness of embeddings from multiple simple source tasks on a single target task. We select coreference resolution, a linguistically complex problem requiring contextual understanding, as focus target task, and test the usefulness of embeddings from comparably simpler tasks tasks such as paraphrase detection, named entity recognition, and relation extraction. Through systematic experiments, we evaluate the impact of individual and combined task embeddings. Our findings reveal that task embeddings vary significantly in utility for coreference resolution, with semantic similarity tasks (e.g., paraphrase detection) proving most beneficial. Additionally, representations from intermediate layers of fine-tuned models often outperform those from final layers. Combining embeddings from multiple tasks consistently improves performance, with attention-based aggregation yielding substantial gains. These insights shed light on relationships between task-specific representations and their adaptability to complex downstream tasks, encouraging further exploration of embedding-level task transfer.

LowFER: Low-rank Bilinear Pooling for Link Prediction

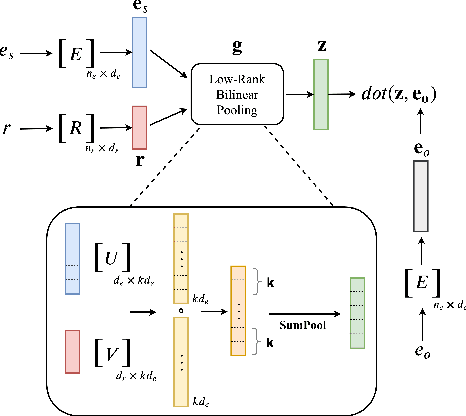
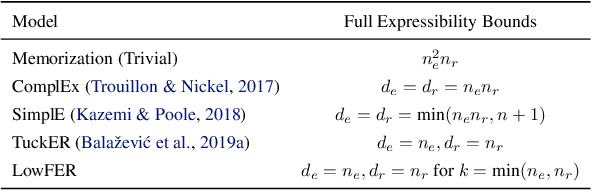
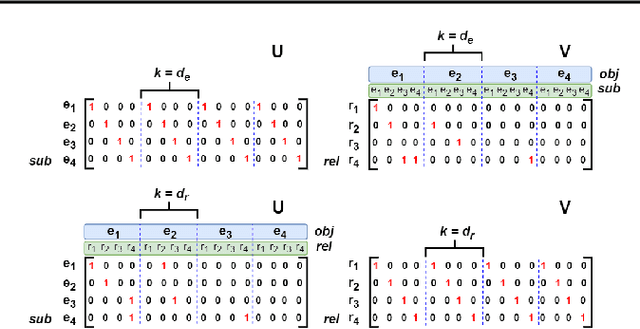
Knowledge graphs are incomplete by nature, with only a limited number of observed facts from the world knowledge being represented as structured relations between entities. To partly address this issue, an important task in statistical relational learning is that of link prediction or knowledge graph completion. Both linear and non-linear models have been proposed to solve the problem. Bilinear models, while expressive, are prone to overfitting and lead to quadratic growth of parameters in number of relations. Simpler models have become more standard, with certain constraints on bilinear map as relation parameters. In this work, we propose a factorized bilinear pooling model, commonly used in multi-modal learning, for better fusion of entities and relations, leading to an efficient and constraint-free model. We prove that our model is fully expressive, providing bounds on the embedding dimensionality and factorization rank. Our model naturally generalizes Tucker decomposition based TuckER model, which has been shown to generalize other models, as efficient low-rank approximation without substantially compromising the performance. Due to low-rank approximation, the model complexity can be controlled by the factorization rank, avoiding the possible cubic growth of TuckER. Empirically, we evaluate on real-world datasets, reaching on par or state-of-the-art performance. At extreme low-ranks, model preserves the performance while staying parameter efficient.