Indian Buffet Process Deep Generative Models for Semi-Supervised Classification

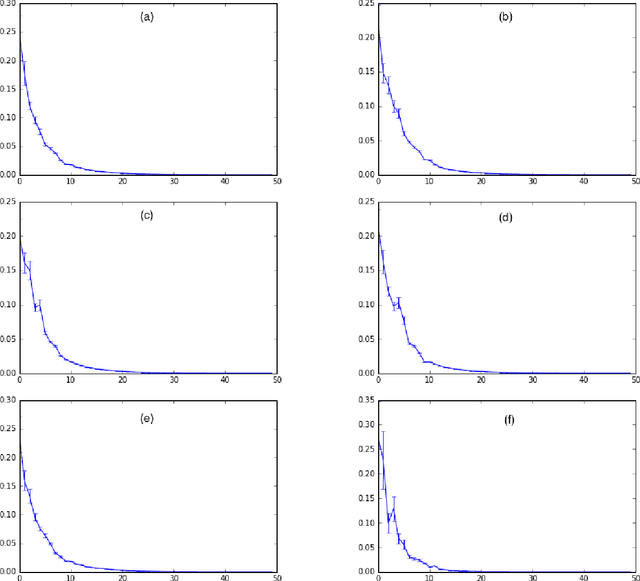
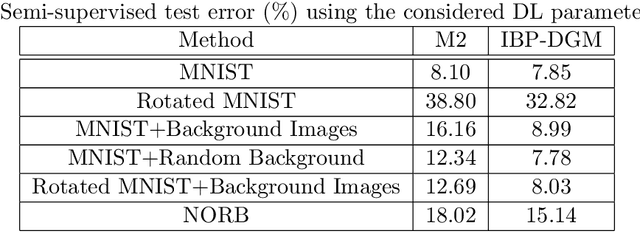
Deep generative models (DGMs) have brought about a major breakthrough, as well as renewed interest, in generative latent variable models. However, DGMs do not allow for performing data-driven inference of the number of latent features needed to represent the observed data. Traditional linear formulations address this issue by resorting to tools from the field of nonparametric statistics. Indeed, linear latent variable models imposed an Indian Buffet Process (IBP) prior have been extensively studied by the machine learning community; inference for such models can been performed either via exact sampling or via approximate variational techniques. Based on this inspiration, in this paper we examine whether similar ideas from the field of Bayesian nonparametrics can be utilized in the context of modern DGMs in order to address the latent variable dimensionality inference problem. To this end, we propose a novel DGM formulation, based on the imposition of an IBP prior. We devise an efficient Black-Box Variational inference algorithm for our model, and exhibit its efficacy in a number of semi-supervised classification experiments. In all cases, we use popular benchmark datasets, and compare to state-of-the-art DGMs.

Deep Network Regularization via Bayesian Inference of Synaptic Connectivity

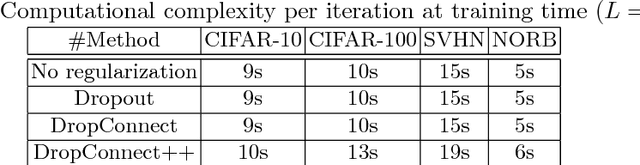
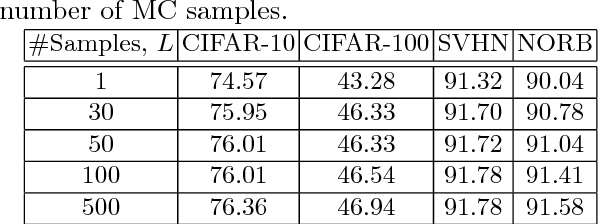
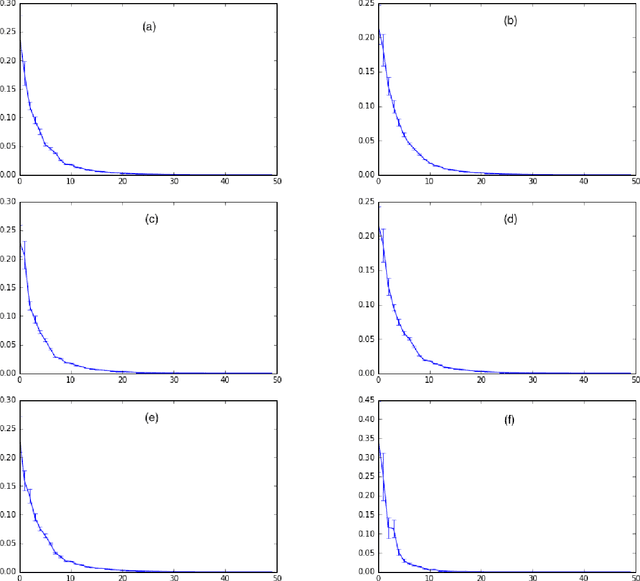
Deep neural networks (DNNs) often require good regularizers to generalize well. Currently, state-of-the-art DNN regularization techniques consist in randomly dropping units and/or connections on each iteration of the training algorithm. Dropout and DropConnect are characteristic examples of such regularizers, that are widely popular among practitioners. However, a drawback of such approaches consists in the fact that their postulated probability of random unit/connection omission is a constant that must be heuristically selected based on the obtained performance in some validation set. To alleviate this burden, in this paper we regard the DNN regularization problem from a Bayesian inference perspective: We impose a sparsity-inducing prior over the network synaptic weights, where the sparsity is induced by a set of Bernoulli-distributed binary variables with Beta (hyper-)priors over their prior parameters. This way, we eventually allow for marginalizing over the DNN synaptic connectivity for output generation, thus giving rise to an effective, heuristics-free, network regularization scheme. We perform Bayesian inference for the resulting hierarchical model by means of an efficient Black-Box Variational inference scheme. We exhibit the advantages of our method over existing approaches by conducting an extensive experimental evaluation using benchmark datasets.

A Nonparametric Bayesian Approach Toward Stacked Convolutional Independent Component Analysis

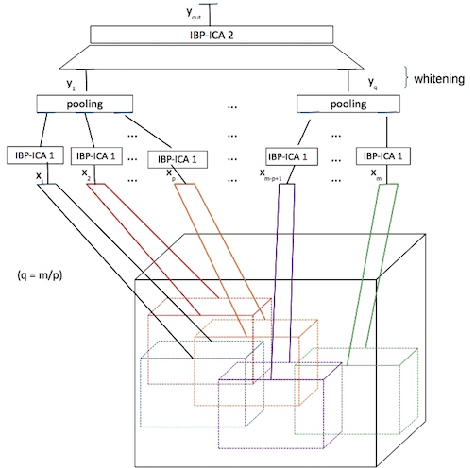
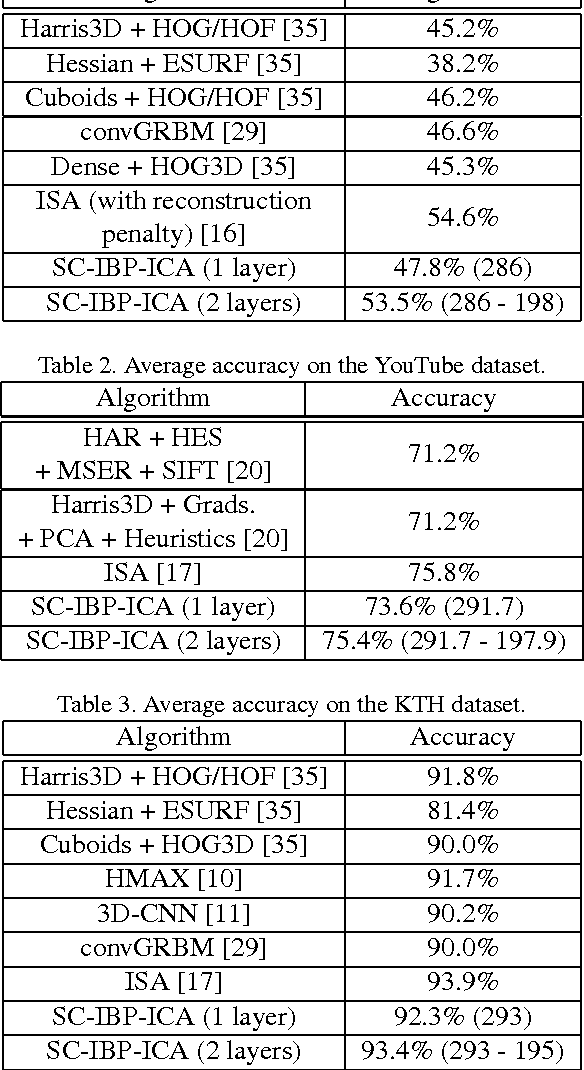
Unsupervised feature learning algorithms based on convolutional formulations of independent components analysis (ICA) have been demonstrated to yield state-of-the-art results in several action recognition benchmarks. However, existing approaches do not allow for the number of latent components (features) to be automatically inferred from the data in an unsupervised manner. This is a significant disadvantage of the state-of-the-art, as it results in considerable burden imposed on researchers and practitioners, who must resort to tedious cross-validation procedures to obtain the optimal number of latent features. To resolve these issues, in this paper we introduce a convolutional nonparametric Bayesian sparse ICA architecture for overcomplete feature learning from high-dimensional data. Our method utilizes an Indian buffet process prior to facilitate inference of the appropriate number of latent features under a hybrid variational inference algorithm, scalable to massive datasets. As we show, our model can be naturally used to obtain deep unsupervised hierarchical feature extractors, by greedily stacking successive model layers, similar to existing approaches. In addition, inference for this model is completely heuristics-free; thus, it obviates the need of tedious parameter tuning, which is a major challenge most deep learning approaches are faced with. We evaluate our method on several action recognition benchmarks, and exhibit its advantages over the state-of-the-art.

Mixture Gaussian Process Conditional Heteroscedasticity

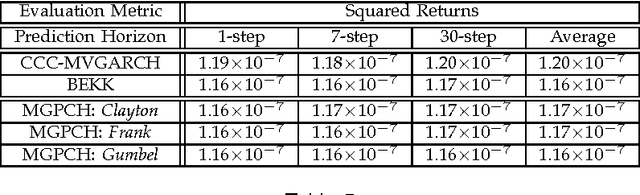
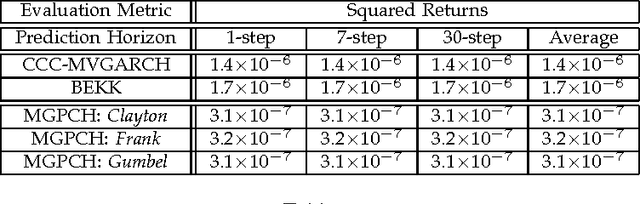
Generalized autoregressive conditional heteroscedasticity (GARCH) models have long been considered as one of the most successful families of approaches for volatility modeling in financial return series. In this paper, we propose an alternative approach based on methodologies widely used in the field of statistical machine learning. Specifically, we propose a novel nonparametric Bayesian mixture of Gaussian process regression models, each component of which models the noise variance process that contaminates the observed data as a separate latent Gaussian process driven by the observed data. This way, we essentially obtain a mixture Gaussian process conditional heteroscedasticity (MGPCH) model for volatility modeling in financial return series. We impose a nonparametric prior with power-law nature over the distribution of the model mixture components, namely the Pitman-Yor process prior, to allow for better capturing modeled data distributions with heavy tails and skewness. Finally, we provide a copula- based approach for obtaining a predictive posterior for the covariances over the asset returns modeled by means of a postulated MGPCH model. We evaluate the efficacy of our approach in a number of benchmark scenarios, and compare its performance to state-of-the-art methodologies.

The Kernel Pitman-Yor Process

In this work, we propose the kernel Pitman-Yor process (KPYP) for nonparametric clustering of data with general spatial or temporal interdependencies. The KPYP is constructed by first introducing an infinite sequence of random locations. Then, based on the stick-breaking construction of the Pitman-Yor process, we define a predictor-dependent random probability measure by considering that the discount hyperparameters of the Beta-distributed random weights (stick variables) of the process are not uniform among the weights, but controlled by a kernel function expressing the proximity between the location assigned to each weight and the given predictors.