Indian Buffet Process Deep Generative Models for Semi-Supervised Classification
Paper and Code
Mar 31, 2018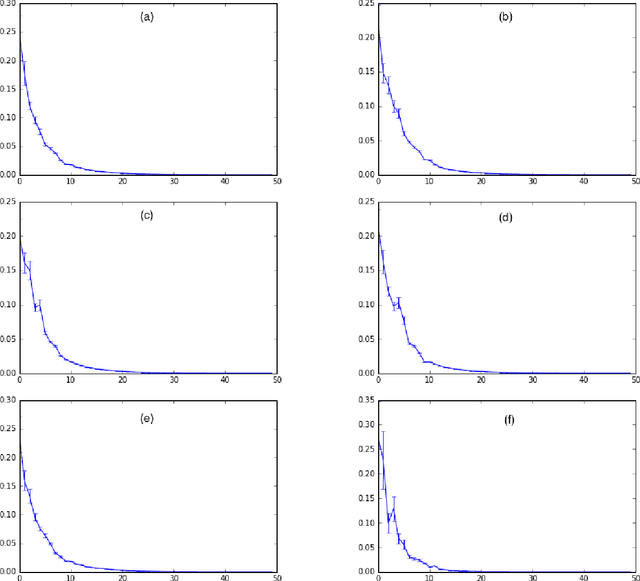
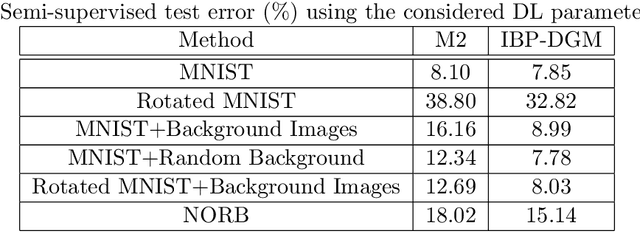

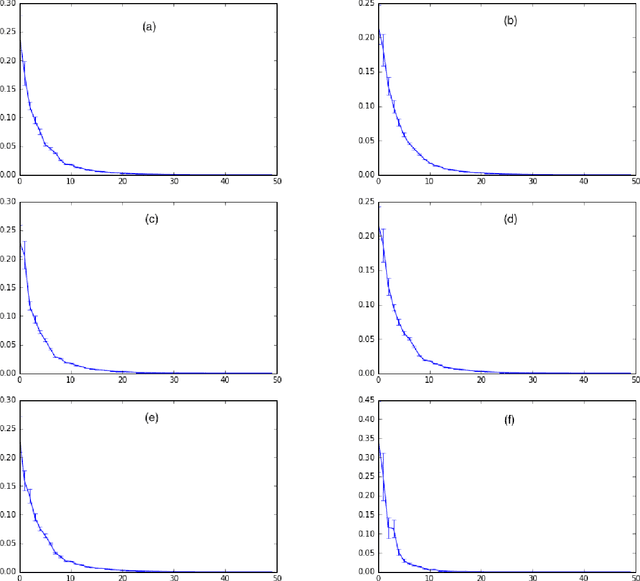
Deep generative models (DGMs) have brought about a major breakthrough, as well as renewed interest, in generative latent variable models. However, DGMs do not allow for performing data-driven inference of the number of latent features needed to represent the observed data. Traditional linear formulations address this issue by resorting to tools from the field of nonparametric statistics. Indeed, linear latent variable models imposed an Indian Buffet Process (IBP) prior have been extensively studied by the machine learning community; inference for such models can been performed either via exact sampling or via approximate variational techniques. Based on this inspiration, in this paper we examine whether similar ideas from the field of Bayesian nonparametrics can be utilized in the context of modern DGMs in order to address the latent variable dimensionality inference problem. To this end, we propose a novel DGM formulation, based on the imposition of an IBP prior. We devise an efficient Black-Box Variational inference algorithm for our model, and exhibit its efficacy in a number of semi-supervised classification experiments. In all cases, we use popular benchmark datasets, and compare to state-of-the-art DGMs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge