Deep Network Regularization via Bayesian Inference of Synaptic Connectivity
Paper and Code
Mar 04, 2018

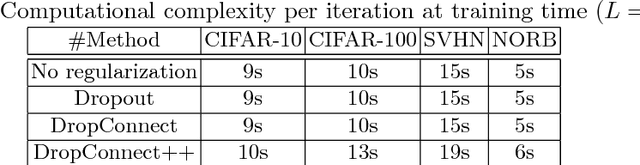
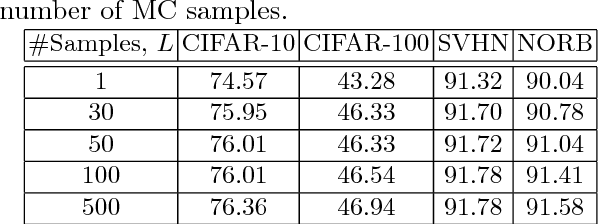
Deep neural networks (DNNs) often require good regularizers to generalize well. Currently, state-of-the-art DNN regularization techniques consist in randomly dropping units and/or connections on each iteration of the training algorithm. Dropout and DropConnect are characteristic examples of such regularizers, that are widely popular among practitioners. However, a drawback of such approaches consists in the fact that their postulated probability of random unit/connection omission is a constant that must be heuristically selected based on the obtained performance in some validation set. To alleviate this burden, in this paper we regard the DNN regularization problem from a Bayesian inference perspective: We impose a sparsity-inducing prior over the network synaptic weights, where the sparsity is induced by a set of Bernoulli-distributed binary variables with Beta (hyper-)priors over their prior parameters. This way, we eventually allow for marginalizing over the DNN synaptic connectivity for output generation, thus giving rise to an effective, heuristics-free, network regularization scheme. We perform Bayesian inference for the resulting hierarchical model by means of an efficient Black-Box Variational inference scheme. We exhibit the advantages of our method over existing approaches by conducting an extensive experimental evaluation using benchmark datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge