Differentiable Collision Avoidance Using Collision Primitives

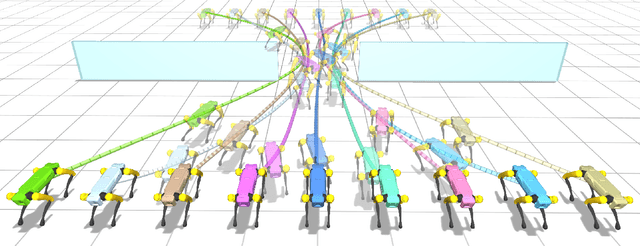
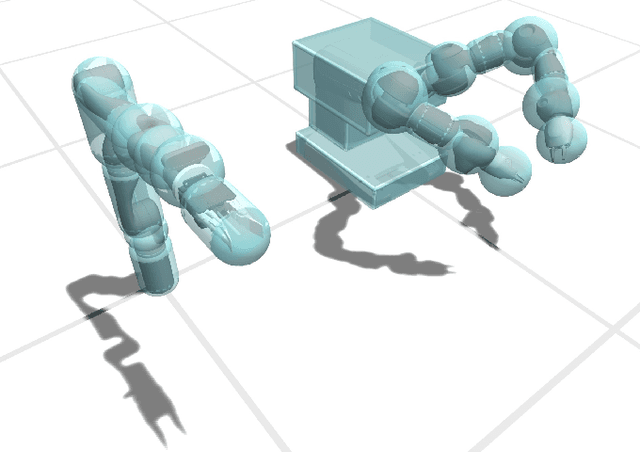
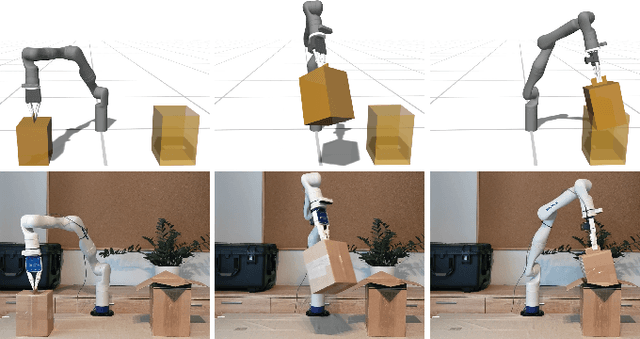
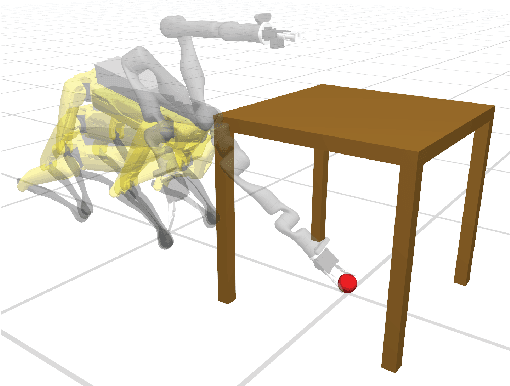
A central aspect of robotic motion planning is collision avoidance, where a multitude of different approaches are currently in use. Optimization-based motion planning is one method, that often heavily relies on distance computations between robots and obstacles. These computations can easily become a bottleneck, as they do not scale well with the complexity of the robots or the environment. To improve performance, many different methods suggested to use collision primitives, i.e. simple shapes that approximate the more complex rigid bodies, and that are simpler to compute distances to and from. However, each pair of primitives requires its own specialized code, and certain pairs are known to suffer from numerical issues. In this paper, we propose an easy-to-use, unified treatment of a wide variety of primitives. We formulate distance computation as a minimization problem, which we solve iteratively. We show how to take derivatives of this minimization problem, allowing it to be seamlessly integrated into a trajectory optimization method. Our experiments show that our method performs favourably, both in terms of timing and the quality of the trajectory. The source code of our implementation will be released upon acceptance.

Trajectory Optimization Using Neural Network Gradients of Learned Dynamics

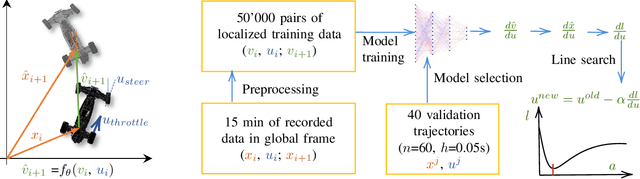
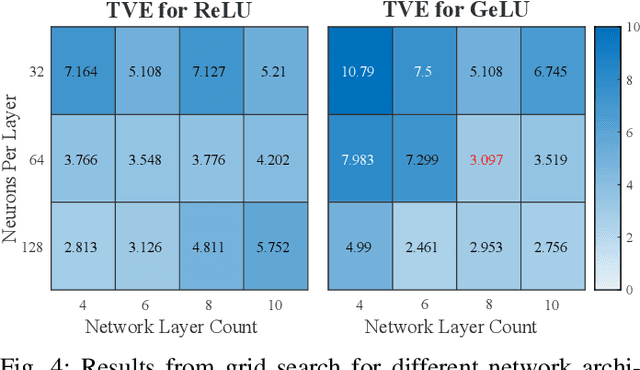
Trajectory optimization methods have achieved an exceptional level of performance on real-world robots in recent years. These methods heavily rely on accurate physics simulators, yet some aspects of the physical world, such as friction, can only be captured to a limited extent by most simulators. The goal of this paper is to leverage trajectory optimization for performing highly dynamic and complex tasks with robotic systems in absence of an accurate physics simulator. This is achieved by applying machine learning techniques to learn a differentiable dynamics model of the system from data. On the example of a RC car, we show that from data collected in only 15 minutes of human-operated interactions with the car, a neural network is able to model highly nonlinear behaviors such as loss of traction and drifting. Furthermore, we use the analytical gradients of the neural network to perform gradient-based trajectory optimization, both in an offline and online setting. We find that our learned model is able to represent complex physical behavior, like drifting and gives unprecedented performance in combination with trajectory optimization methods.