Differentiable Collision Avoidance Using Collision Primitives
Paper and Code
Apr 20, 2022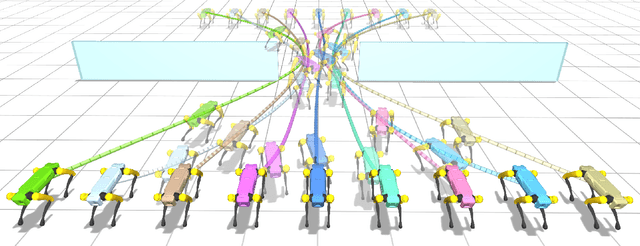
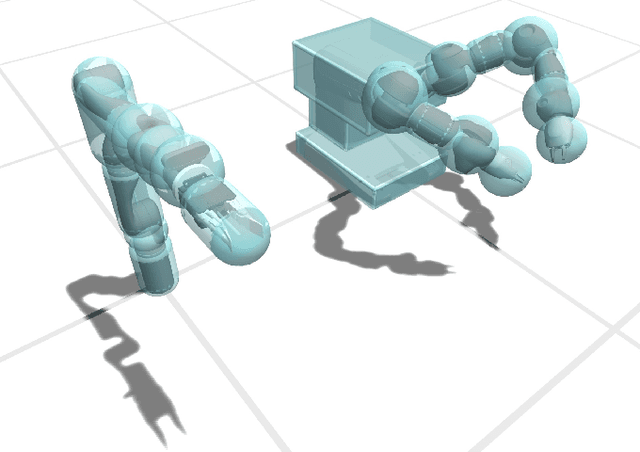
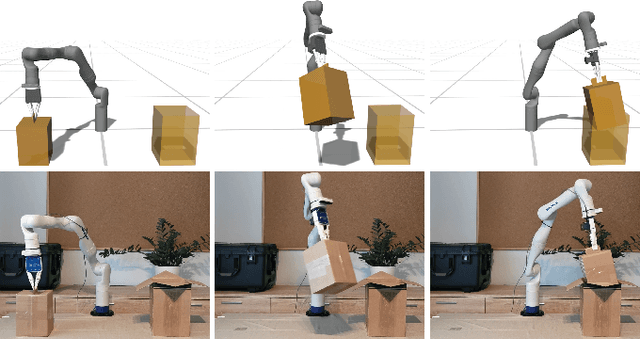
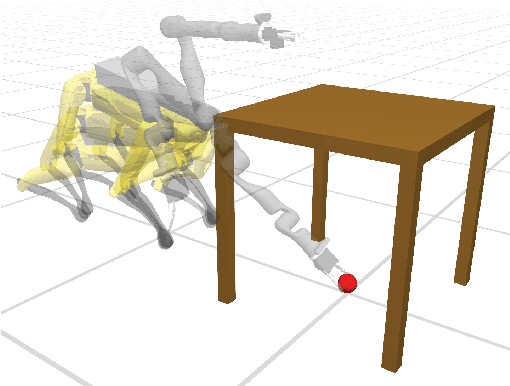
A central aspect of robotic motion planning is collision avoidance, where a multitude of different approaches are currently in use. Optimization-based motion planning is one method, that often heavily relies on distance computations between robots and obstacles. These computations can easily become a bottleneck, as they do not scale well with the complexity of the robots or the environment. To improve performance, many different methods suggested to use collision primitives, i.e. simple shapes that approximate the more complex rigid bodies, and that are simpler to compute distances to and from. However, each pair of primitives requires its own specialized code, and certain pairs are known to suffer from numerical issues. In this paper, we propose an easy-to-use, unified treatment of a wide variety of primitives. We formulate distance computation as a minimization problem, which we solve iteratively. We show how to take derivatives of this minimization problem, allowing it to be seamlessly integrated into a trajectory optimization method. Our experiments show that our method performs favourably, both in terms of timing and the quality of the trajectory. The source code of our implementation will be released upon acceptance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge