Neural varifolds: an aggregate representation for quantifying the geometry of point clouds

Point clouds are popular 3D representations for real-life objects (such as in LiDAR and Kinect) due to their detailed and compact representation of surface-based geometry. Recent approaches characterise the geometry of point clouds by bringing deep learning based techniques together with geometric fidelity metrics such as optimal transportation costs (e.g., Chamfer and Wasserstein metrics). In this paper, we propose a new surface geometry characterisation within this realm, namely a neural varifold representation of point clouds. Here the surface is represented as a measure/distribution over both point positions and tangent spaces of point clouds. The varifold representation quantifies not only the surface geometry of point clouds through the manifold-based discrimination, but also subtle geometric consistencies on the surface due to the combined product space. This study proposes neural varifold algorithms to compute the varifold norm between two point clouds using neural networks on point clouds and their neural tangent kernel representations. The proposed neural varifold is evaluated on three different sought-after tasks -- shape matching, few-shot shape classification and shape reconstruction. Detailed evaluation and comparison to the state-of-the-art methods demonstrate that the proposed versatile neural varifold is superior in shape matching and few-shot shape classification, and is competitive for shape reconstruction.

A linear framework for region-based image segmentation and inpainting involving curvature penalization

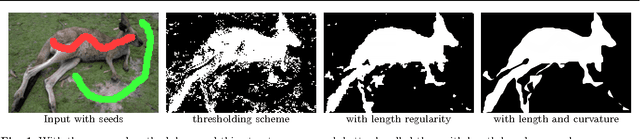
We present the first method to handle curvature regularity in region-based image segmentation and inpainting that is independent of initialization. To this end we start from a new formulation of length-based optimization schemes, based on surface continuation constraints, and discuss the connections to existing schemes. The formulation is based on a \emph{cell complex} and considers basic regions and boundary elements. The corresponding optimization problem is cast as an integer linear program. We then show how the method can be extended to include curvature regularity, again cast as an integer linear program. Here, we are considering pairs of boundary elements to reflect curvature. Moreover, a constraint set is derived to ensure that the boundary variables indeed reflect the boundary of the regions described by the region variables. We show that by solving the linear programming relaxation one gets quite close to the global optimum, and that curvature regularity is indeed much better suited in the presence of long and thin objects compared to standard length regularity.