Thomas Schoenemann
Generalized sequential tree-reweighted message passing
Sep 13, 2012



Abstract:This paper addresses the problem of approximate MAP-MRF inference in general graphical models. Following [36], we consider a family of linear programming relaxations of the problem where each relaxation is specified by a set of nested pairs of factors for which the marginalization constraint needs to be enforced. We develop a generalization of the TRW-S algorithm [9] for this problem, where we use a decomposition into junction chains, monotonic w.r.t. some ordering on the nodes. This generalizes the monotonic chains in [9] in a natural way. We also show how to deal with nested factors in an efficient way. Experiments show an improvement over min-sum diffusion, MPLP and subgradient ascent algorithms on a number of computer vision and natural language processing problems.
A linear framework for region-based image segmentation and inpainting involving curvature penalization
Feb 18, 2011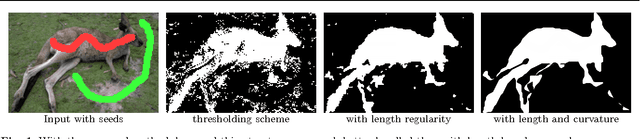



Abstract:We present the first method to handle curvature regularity in region-based image segmentation and inpainting that is independent of initialization. To this end we start from a new formulation of length-based optimization schemes, based on surface continuation constraints, and discuss the connections to existing schemes. The formulation is based on a \emph{cell complex} and considers basic regions and boundary elements. The corresponding optimization problem is cast as an integer linear program. We then show how the method can be extended to include curvature regularity, again cast as an integer linear program. Here, we are considering pairs of boundary elements to reflect curvature. Moreover, a constraint set is derived to ensure that the boundary variables indeed reflect the boundary of the regions described by the region variables. We show that by solving the linear programming relaxation one gets quite close to the global optimum, and that curvature regularity is indeed much better suited in the presence of long and thin objects compared to standard length regularity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge