Content Prompting: Modeling Content Provider Dynamics to Improve User Welfare in Recommender Ecosystems

Users derive value from a recommender system (RS) only to the extent that it is able to surface content (or items) that meet their needs/preferences. While RSs often have a comprehensive view of user preferences across the entire user base, content providers, by contrast, generally have only a local view of the preferences of users that have interacted with their content. This limits a provider's ability to offer new content to best serve the broader population. In this work, we tackle this information asymmetry with content prompting policies. A content prompt is a hint or suggestion to a provider to make available novel content for which the RS predicts unmet user demand. A prompting policy is a sequence of such prompts that is responsive to the dynamics of a provider's beliefs, skills and incentives. We aim to determine a joint prompting policy that induces a set of providers to make content available that optimizes user social welfare in equilibrium, while respecting the incentives of the providers themselves. Our contributions include: (i) an abstract model of the RS ecosystem, including content provider behaviors, that supports such prompting; (ii) the design and theoretical analysis of sequential prompting policies for individual providers; (iii) a mixed integer programming formulation for optimal joint prompting using path planning in content space; and (iv) simple, proof-of-concept experiments illustrating how such policies improve ecosystem health and user welfare.

Structural Analysis of Branch-and-Cut and the Learnability of Gomory Mixed Integer Cuts

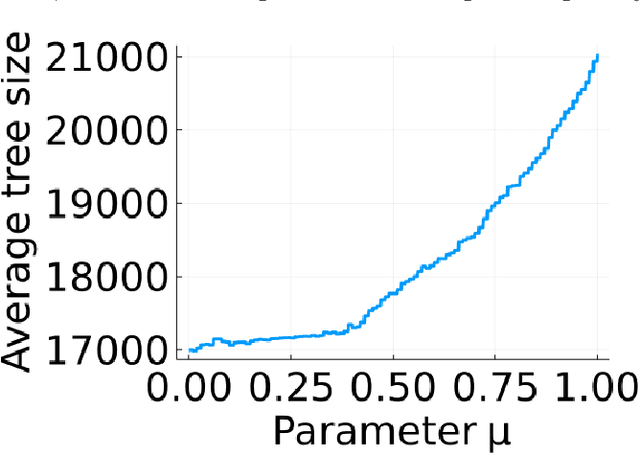
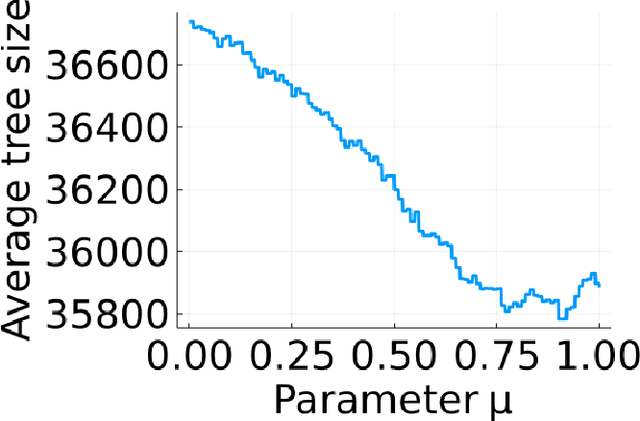
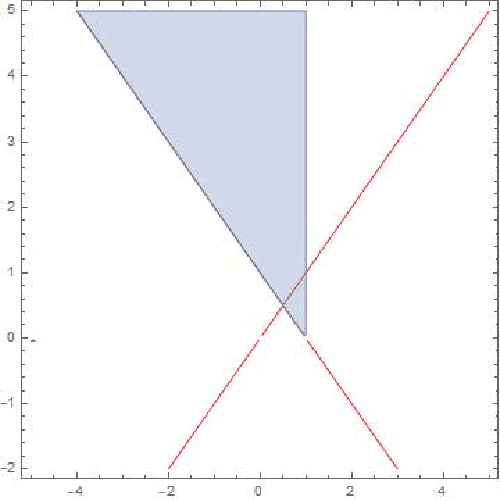
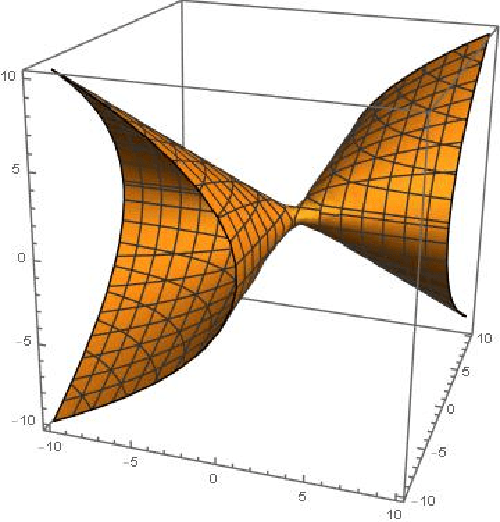
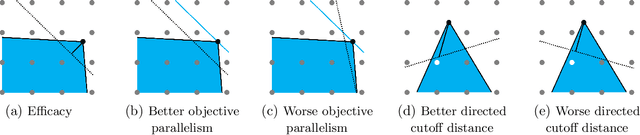
The incorporation of cutting planes within the branch-and-bound algorithm, known as branch-and-cut, forms the backbone of modern integer programming solvers. These solvers are the foremost method for solving discrete optimization problems and thus have a vast array of applications in machine learning, operations research, and many other fields. Choosing cutting planes effectively is a major research topic in the theory and practice of integer programming. We conduct a novel structural analysis of branch-and-cut that pins down how every step of the algorithm is affected by changes in the parameters defining the cutting planes added to the input integer program. Our main application of this analysis is to derive sample complexity guarantees for using machine learning to determine which cutting planes to apply during branch-and-cut. These guarantees apply to infinite families of cutting planes, such as the family of Gomory mixed integer cuts, which are responsible for the main breakthrough speedups of integer programming solvers. We exploit geometric and combinatorial structure of branch-and-cut in our analysis, which provides a key missing piece for the recent generalization theory of branch-and-cut.

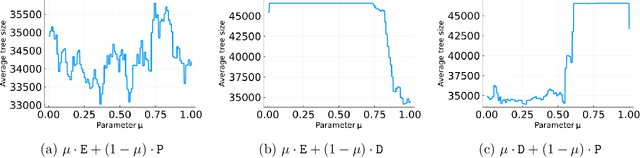
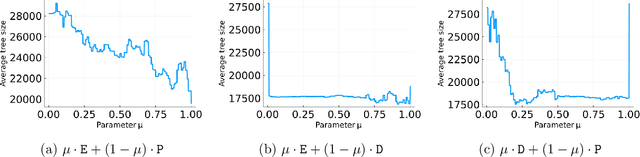
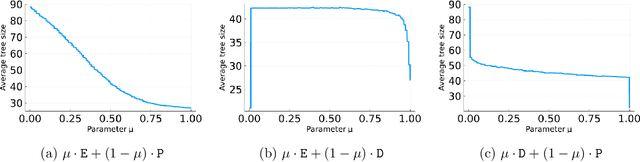
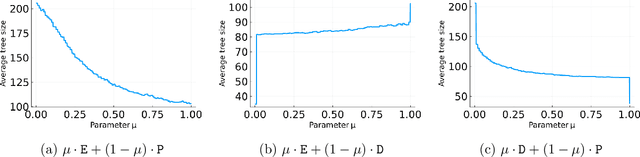
Improved Learning Bounds for Branch-and-Cut

Branch-and-cut is the most widely used algorithm for solving integer programs, employed by commercial solvers like CPLEX and Gurobi. Branch-and-cut has a wide variety of tunable parameters that have a huge impact on the size of the search tree that it builds, but are challenging to tune by hand. An increasingly popular approach is to use machine learning to tune these parameters: using a training set of integer programs from the application domain at hand, the goal is to find a configuration with strong predicted performance on future, unseen integer programs from the same domain. If the training set is too small, a configuration may have good performance over the training set but poor performance on future integer programs. In this paper, we prove sample complexity guarantees for this procedure, which bound how large the training set should be to ensure that for any configuration, its average performance over the training set is close to its expected future performance. Our guarantees apply to parameters that control the most important aspects of branch-and-cut: node selection, branching constraint selection, and cutting plane selection, and are sharper and more general than those found in prior research.

Sample Complexity of Tree Search Configuration: Cutting Planes and Beyond

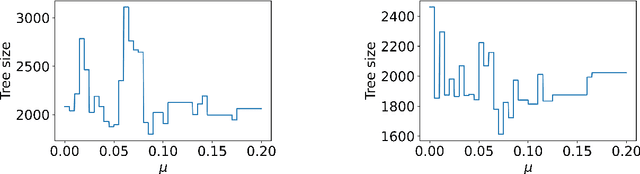
Cutting-plane methods have enabled remarkable successes in integer programming over the last few decades. State-of-the-art solvers integrate a myriad of cutting-plane techniques to speed up the underlying tree-search algorithm used to find optimal solutions. In this paper we prove the first guarantees for learning high-performing cut-selection policies tailored to the instance distribution at hand using samples. We first bound the sample complexity of learning cutting planes from the canonical family of Chv\'atal-Gomory cuts. Our bounds handle any number of waves of any number of cuts and are fine tuned to the magnitudes of the constraint coefficients. Next, we prove sample complexity bounds for more sophisticated cut selection policies that use a combination of scoring rules to choose from a family of cuts. Finally, beyond the realm of cutting planes for integer programming, we develop a general abstraction of tree search that captures key components such as node selection and variable selection. For this abstraction, we bound the sample complexity of learning a good policy for building the search tree.

Incentive Compatible Active Learning

We consider active learning under incentive compatibility constraints. The main application of our results is to economic experiments, in which a learner seeks to infer the parameters of a subject's preferences: for example their attitudes towards risk, or their beliefs over uncertain events. By cleverly adapting the experimental design, one can save on the time spent by subjects in the laboratory, or maximize the information obtained from each subject in a given laboratory session; but the resulting adaptive design raises complications due to incentive compatibility. A subject in the lab may answer questions strategically, and not truthfully, so as to steer subsequent questions in a profitable direction. We analyze two standard economic problems: inference of preferences over risk from multiple price lists, and belief elicitation in experiments on choice over uncertainty. In the first setting, we tune a simple and fast learning algorithm to retain certain incentive compatibility properties. In the second setting, we provide an incentive compatible learning algorithm based on scoring rules with query complexity that differs from obvious methods of achieving fast learning rates only by subpolynomial factors. Thus, for these areas of application, incentive compatibility may be achieved without paying a large sample complexity price.

Learning Time Dependent Choice

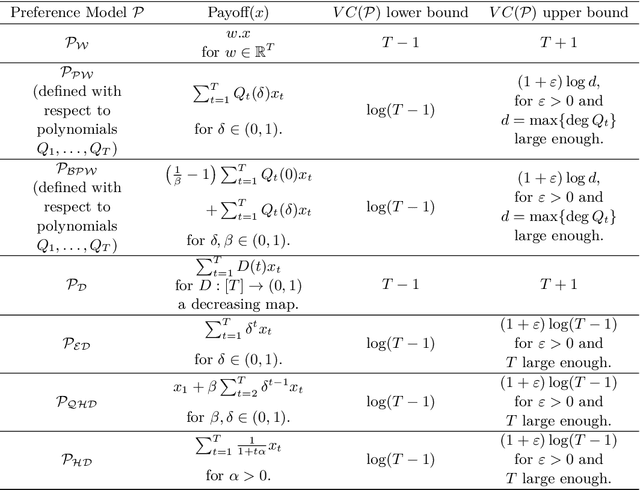
We explore questions dealing with the learnability of models of choice over time. We present a large class of preference models defined by a structural criterion for which we are able to obtain an exponential improvement over previously known learning bounds for more general preference models. This in particular implies that the three most important discounted utility models of intertemporal choice -- exponential, hyperbolic, and quasi-hyperbolic discounting -- are learnable in the PAC setting with VC dimension that grows logarithmically in the number of time periods. We also examine these models in the framework of active learning. We find that the commonly studied stream-based setting is in general difficult to analyze for preference models, but we provide a redeeming situation in which the learner can indeed improve upon the guarantees provided by PAC learning. In contrast to the stream-based setting, we show that if the learner is given full power over the data he learns from -- in the form of learning via membership queries -- even very naive algorithms significantly outperform the guarantees provided by higher level active learning algorithms.