Improved Learning Bounds for Branch-and-Cut

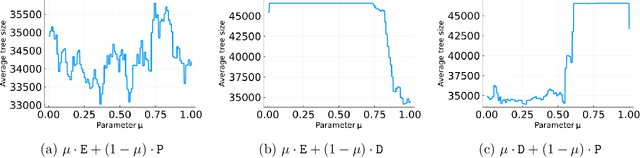
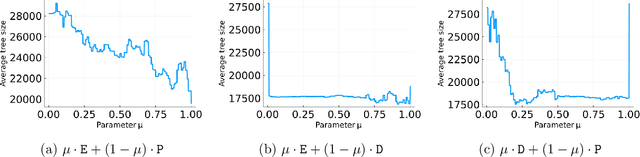
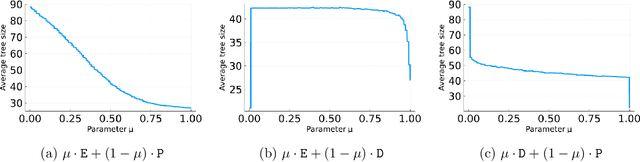
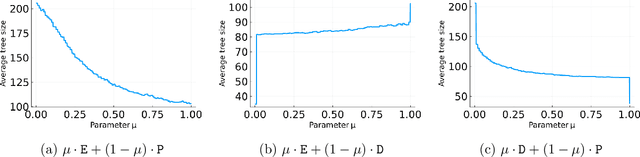
Branch-and-cut is the most widely used algorithm for solving integer programs, employed by commercial solvers like CPLEX and Gurobi. Branch-and-cut has a wide variety of tunable parameters that have a huge impact on the size of the search tree that it builds, but are challenging to tune by hand. An increasingly popular approach is to use machine learning to tune these parameters: using a training set of integer programs from the application domain at hand, the goal is to find a configuration with strong predicted performance on future, unseen integer programs from the same domain. If the training set is too small, a configuration may have good performance over the training set but poor performance on future integer programs. In this paper, we prove sample complexity guarantees for this procedure, which bound how large the training set should be to ensure that for any configuration, its average performance over the training set is close to its expected future performance. Our guarantees apply to parameters that control the most important aspects of branch-and-cut: node selection, branching constraint selection, and cutting plane selection, and are sharper and more general than those found in prior research.