Large scale representation learning from triplet comparisons

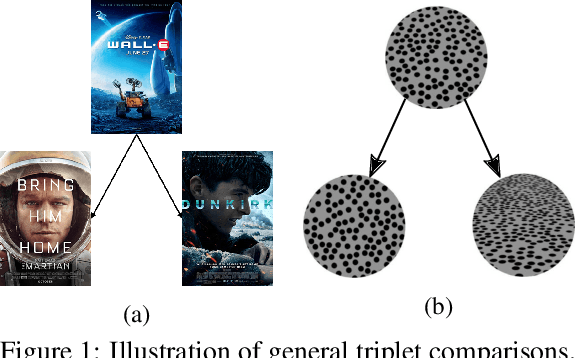
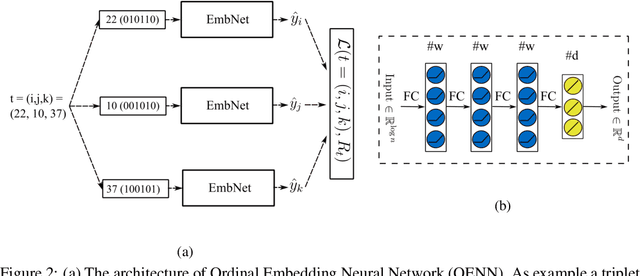
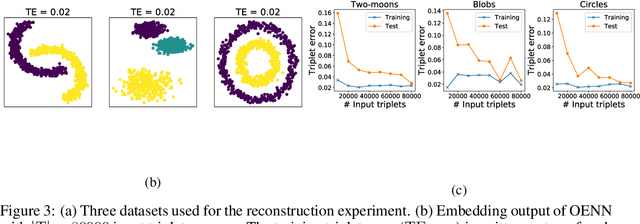
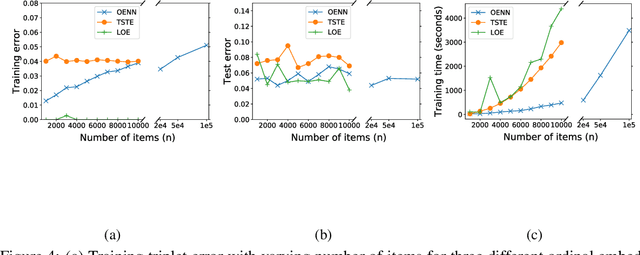
In this paper, we discuss the fundamental problem of representation learning from a new perspective. It has been observed in many supervised/unsupervised DNNs that the final layer of the network often provides an informative representation for many tasks, even though the network has been trained to perform a particular task. The common ingredient in all previous studies is a low-level feature representation for items, for example, RGB values of images in the image context. In the present work, we assume that no meaningful representation of the items is given. Instead, we are provided with the answers to some triplet comparisons of the following form: Is item A more similar to item B or item C? We provide a fast algorithm based on DNNs that constructs a Euclidean representation for the items, using solely the answers to the above-mentioned triplet comparisons. This problem has been studied in a sub-community of machine learning by the name "Ordinal Embedding". Previous approaches to the problem are painfully slow and cannot scale to larger datasets. We demonstrate that our proposed approach is significantly faster than available methods, and can scale to real-world large datasets. Thereby, we also draw attention to the less explored idea of using neural networks to directly, approximately solve non-convex, NP-hard optimization problems that arise naturally in unsupervised learning problems.

Estimation of perceptual scales using ordinal embedding

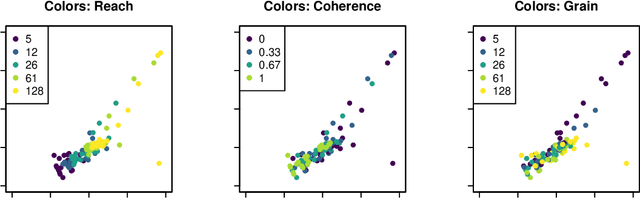
In this paper, we address the problem of measuring and analysing sensation, the subjective magnitude of one's experience. We do this in the context of the method of triads: the sensation of the stimulus is evaluated via relative judgments of the form: "Is stimulus S_i more similar to stimulus S_j or to stimulus S_k?". We propose to use ordinal embedding methods from machine learning to estimate the scaling function from the relative judgments. We review two relevant and well-known methods in psychophysics which are partially applicable in our setting: non-metric multi-dimensional scaling (NMDS) and the method of maximum likelihood difference scaling (MLDS). We perform an extensive set of simulations, considering various scaling functions, to demonstrate the performance of the ordinal embedding methods. We show that in contrast to existing approaches our ordinal embedding approach allows, first, to obtain reasonable scaling function from comparatively few relative judgments, second, the estimation of non-monotonous scaling functions, and, third, multi-dimensional perceptual scales. In addition to the simulations, we analyse data from two real psychophysics experiments using ordinal embedding methods. Our results show that in the one-dimensional, monotonically increasing perceptual scale our ordinal embedding approach works as well as MLDS, while in higher dimensions, only our ordinal embedding methods can produce a desirable scaling function. To make our methods widely accessible, we provide an R-implementation and general rules of thumb on how to use ordinal embedding in the context of psychophysics.

Comparison-Based Framework for Psychophysics: Lab versus Crowdsourcing

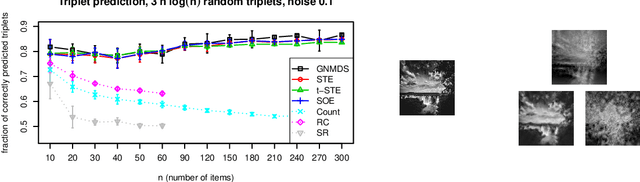
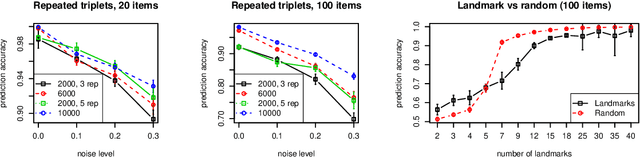
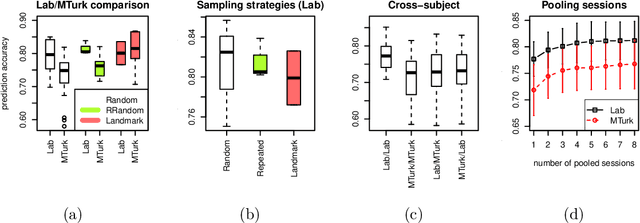
Traditionally, psychophysical experiments are conducted by repeated measurements on a few well-trained participants under well-controlled conditions, often resulting in, if done properly, high quality data. In recent years, however, crowdsourcing platforms are becoming increasingly popular means of data collection, measuring many participants at the potential cost of obtaining data of worse quality. In this paper we study whether the use of comparison-based (ordinal) data, combined with machine learning algorithms, can boost the reliability of crowdsourcing studies for psychophysics, such that they can achieve performance close to a lab experiment. To this end, we compare three setups: simulations, a psychophysics lab experiment, and the same experiment on Amazon Mechanical Turk. All these experiments are conducted in a comparison-based setting where participants have to answer triplet questions of the form "is object x closer to y or to z?". We then use machine learning to solve the triplet prediction problem: given a subset of triplet questions with corresponding answers, we predict the answer to the remaining questions. Considering the limitations and noise on MTurk, we find that the accuracy of triplet prediction is surprisingly close---but not equal---to our lab study.

Comparison-Based Random Forests

Assume we are given a set of items from a general metric space, but we neither have access to the representation of the data nor to the distances between data points. Instead, suppose that we can actively choose a triplet of items (A,B,C) and ask an oracle whether item A is closer to item B or to item C. In this paper, we propose a novel random forest algorithm for regression and classification that relies only on such triplet comparisons. In the theory part of this paper, we establish sufficient conditions for the consistency of such a forest. In a set of comprehensive experiments, we then demonstrate that the proposed random forest is efficient both for classification and regression. In particular, it is even competitive with other methods that have direct access to the metric representation of the data.

Comparison Based Nearest Neighbor Search

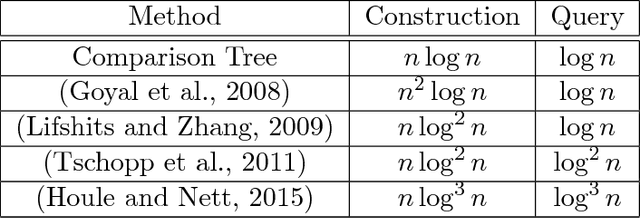
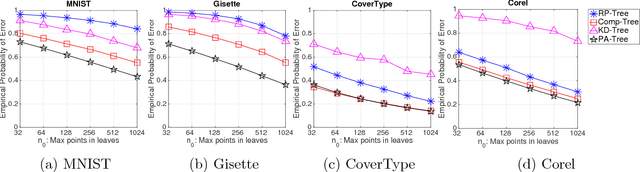
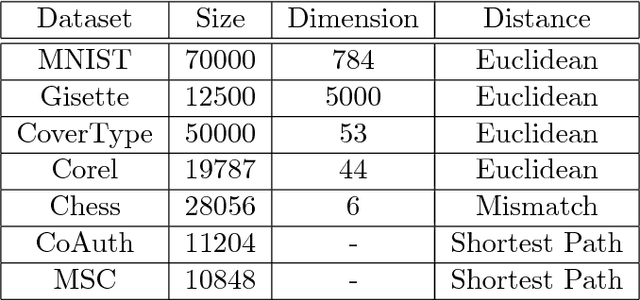
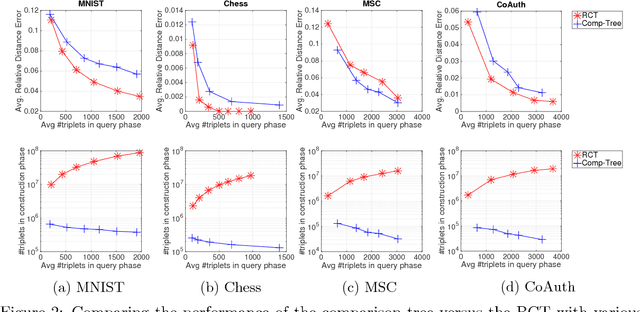
We consider machine learning in a comparison-based setting where we are given a set of points in a metric space, but we have no access to the actual distances between the points. Instead, we can only ask an oracle whether the distance between two points $i$ and $j$ is smaller than the distance between the points $i$ and $k$. We are concerned with data structures and algorithms to find nearest neighbors based on such comparisons. We focus on a simple yet effective algorithm that recursively splits the space by first selecting two random pivot points and then assigning all other points to the closer of the two (comparison tree). We prove that if the metric space satisfies certain expansion conditions, then with high probability the height of the comparison tree is logarithmic in the number of points, leading to efficient search performance. We also provide an upper bound for the failure probability to return the true nearest neighbor. Experiments show that the comparison tree is competitive with algorithms that have access to the actual distance values, and needs less triplet comparisons than other competitors.