Large scale representation learning from triplet comparisons

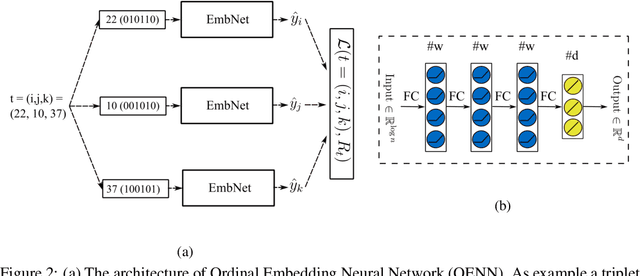
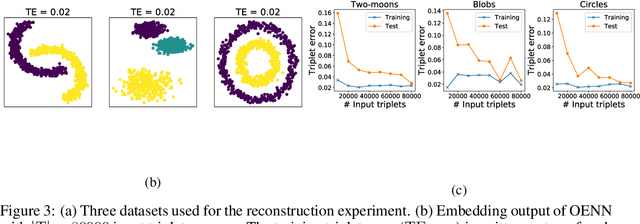
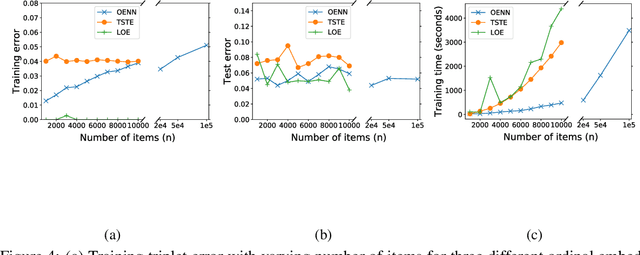
In this paper, we discuss the fundamental problem of representation learning from a new perspective. It has been observed in many supervised/unsupervised DNNs that the final layer of the network often provides an informative representation for many tasks, even though the network has been trained to perform a particular task. The common ingredient in all previous studies is a low-level feature representation for items, for example, RGB values of images in the image context. In the present work, we assume that no meaningful representation of the items is given. Instead, we are provided with the answers to some triplet comparisons of the following form: Is item A more similar to item B or item C? We provide a fast algorithm based on DNNs that constructs a Euclidean representation for the items, using solely the answers to the above-mentioned triplet comparisons. This problem has been studied in a sub-community of machine learning by the name "Ordinal Embedding". Previous approaches to the problem are painfully slow and cannot scale to larger datasets. We demonstrate that our proposed approach is significantly faster than available methods, and can scale to real-world large datasets. Thereby, we also draw attention to the less explored idea of using neural networks to directly, approximately solve non-convex, NP-hard optimization problems that arise naturally in unsupervised learning problems.