Improving Credit Card Fraud Detection with an Optimized Explainable Boosting Machine

Addressing class imbalance is a central challenge in credit card fraud detection, as it directly impacts predictive reliability in real-world financial systems. To overcome this, the study proposes an enhanced workflow based on the Explainable Boosting Machine (EBM)-a transparent, state-of-the-art implementation of the GA2M algorithm-optimized through systematic hyperparameter tuning, feature selection, and preprocessing refinement. Rather than relying on conventional sampling techniques that may introduce bias or cause information loss, the optimized EBM achieves an effective balance between accuracy and interpretability, enabling precise detection of fraudulent transactions while providing actionable insights into feature importance and interaction effects. Furthermore, the Taguchi method is employed to optimize both the sequence of data scalers and model hyperparameters, ensuring robust, reproducible, and systematically validated performance improvements. Experimental evaluation on benchmark credit card data yields an ROC-AUC of 0.983, surpassing prior EBM baselines (0.975) and outperforming Logistic Regression, Random Forest, XGBoost, and Decision Tree models. These results highlight the potential of interpretable machine learning and data-driven optimization for advancing trustworthy fraud analytics in financial systems.

Optimizing the Consumption of Spiking Neural Networks with Activity Regularization

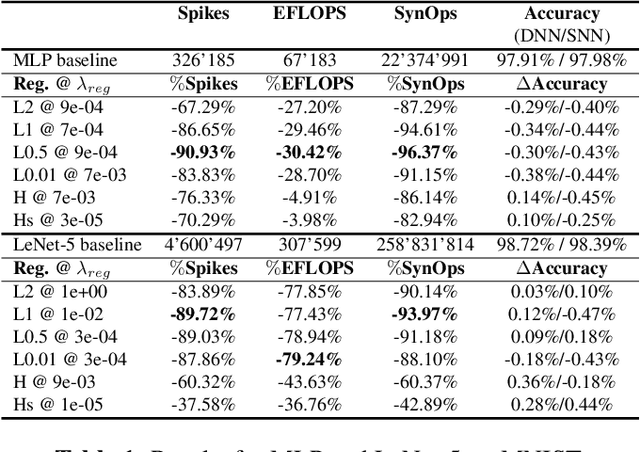
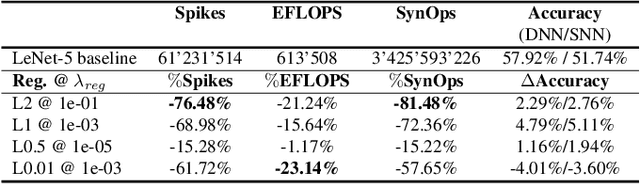
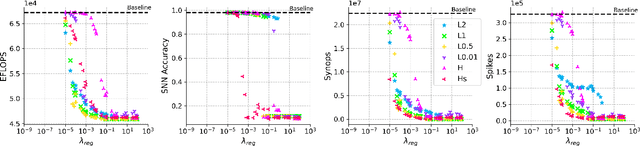
Reducing energy consumption is a critical point for neural network models running on edge devices. In this regard, reducing the number of multiply-accumulate (MAC) operations of Deep Neural Networks (DNNs) running on edge hardware accelerators will reduce the energy consumption during inference. Spiking Neural Networks (SNNs) are an example of bio-inspired techniques that can further save energy by using binary activations, and avoid consuming energy when not spiking. The networks can be configured for equivalent accuracy on a task through DNN-to-SNN conversion frameworks but their conversion is based on rate coding therefore the synaptic operations can be high. In this work, we look into different techniques to enforce sparsity on the neural network activation maps and compare the effect of different training regularizers on the efficiency of the optimized DNNs and SNNs.

Efficient Blind-Spot Neural Network Architecture for Image Denoising

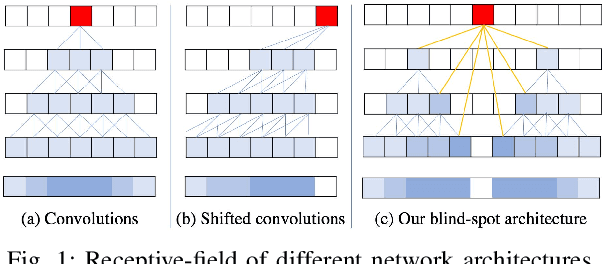
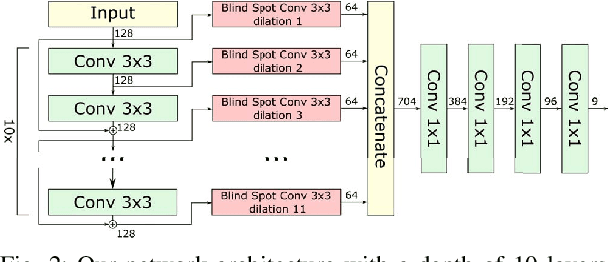
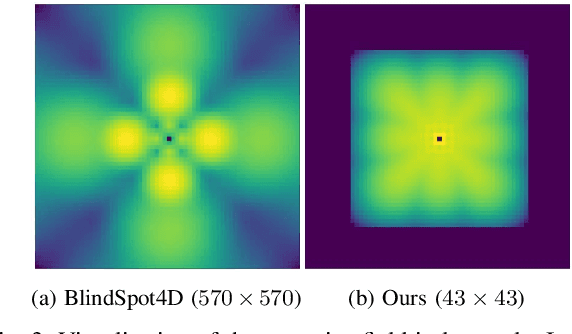
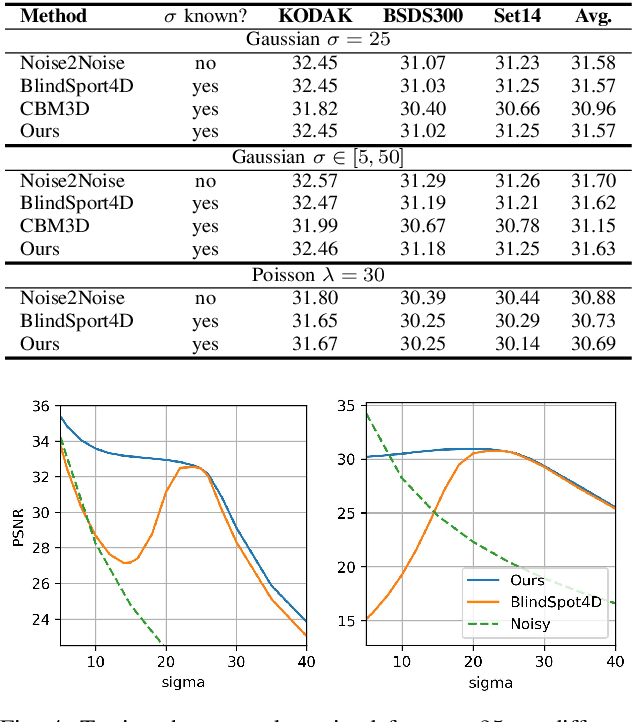
Image denoising is an essential tool in computational photography. Standard denoising techniques, which use deep neural networks at their core, require pairs of clean and noisy images for its training. If we do not possess the clean samples, we can use blind-spot neural network architectures, which estimate the pixel value based on the neighbouring pixels only. These networks thus allow training on noisy images directly, as they by-design avoid trivial solutions. Nowadays, the blind-spot is mostly achieved using shifted convolutions or serialization. We propose a novel fully convolutional network architecture that uses dilations to achieve the blind-spot property. Our network improves the performance over the prior work and achieves state-of-the-art results on established datasets.

Learning Generative Models using Denoising Density Estimators

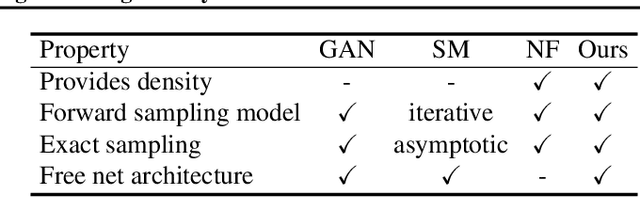
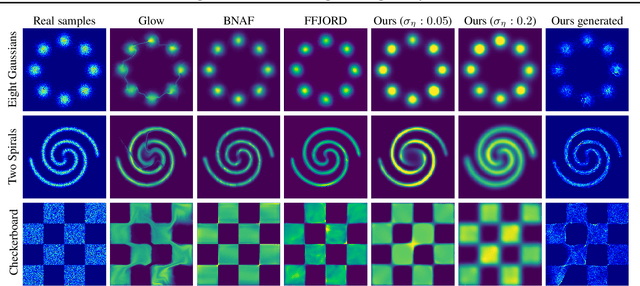
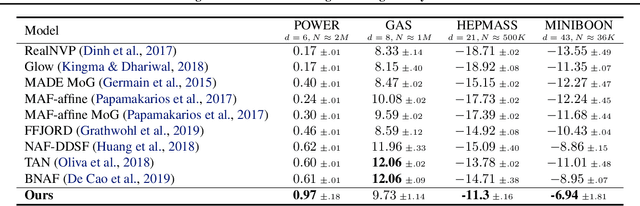
Learning generative probabilistic models that can estimate the continuous density given a set of samples, and that can sample from that density, is one of the fundamental challenges in unsupervised machine learning. In this paper we introduce a new approach to obtain such models based on what we call denoising density estimators (DDEs). A DDE is a scalar function, parameterized by a neural network, that is efficiently trained to represent a kernel density estimator of the data. Leveraging DDEs, our main contribution is to develop a novel approach to obtain generative models that sample from given densities. We prove that our algorithms to obtain both DDEs and generative models are guaranteed to converge to the correct solutions. Advantages of our approach include that we do not require specific network architectures like in normalizing flows, ordinary differential equation solvers as in continuous normalizing flows, nor do we require adversarial training as in generative adversarial networks (GANs). Finally, we provide experimental results that demonstrate practical applications of our technique.