Learning Generative Models using Denoising Density Estimators

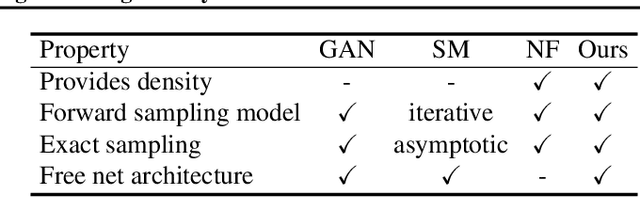
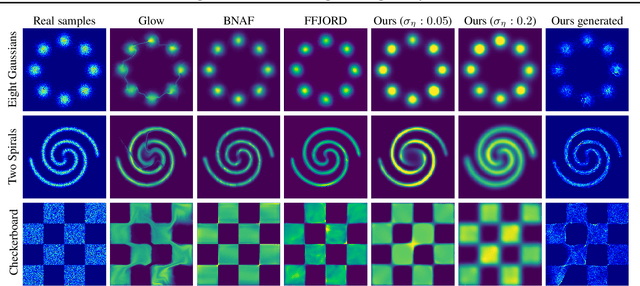
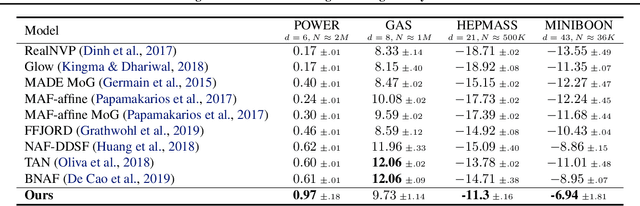
Learning generative probabilistic models that can estimate the continuous density given a set of samples, and that can sample from that density, is one of the fundamental challenges in unsupervised machine learning. In this paper we introduce a new approach to obtain such models based on what we call denoising density estimators (DDEs). A DDE is a scalar function, parameterized by a neural network, that is efficiently trained to represent a kernel density estimator of the data. Leveraging DDEs, our main contribution is to develop a novel approach to obtain generative models that sample from given densities. We prove that our algorithms to obtain both DDEs and generative models are guaranteed to converge to the correct solutions. Advantages of our approach include that we do not require specific network architectures like in normalizing flows, ordinary differential equation solvers as in continuous normalizing flows, nor do we require adversarial training as in generative adversarial networks (GANs). Finally, we provide experimental results that demonstrate practical applications of our technique.