Optimal and Stable Multi-Layer Object Rearrangement on a Tabletop

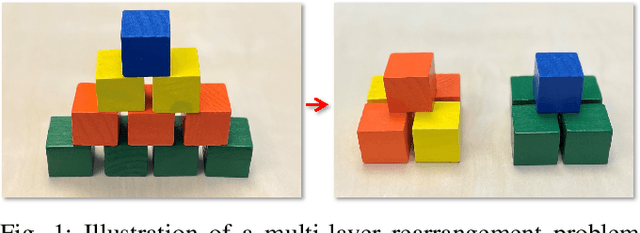
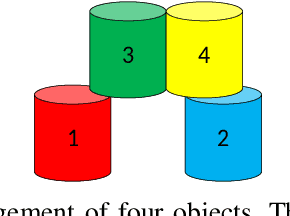
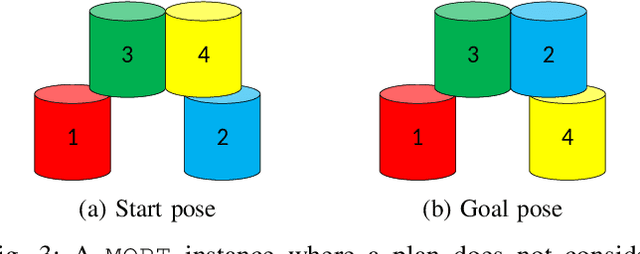
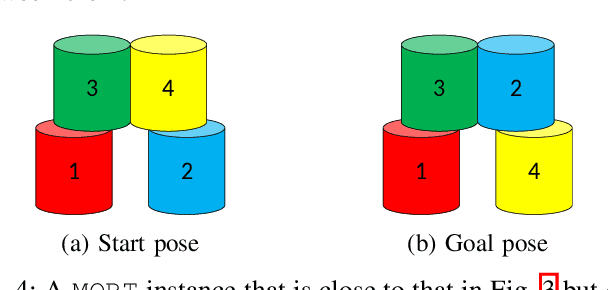
Object rearrangement is a fundamental sub-task in accomplishing a great many physical tasks. As such, effectively executing rearrangement is an important skill for intelligent robots to master. In this study, we conduct the first algorithmic study on optimally solving the problem of Multi-layer Object Rearrangement on a Tabletop (MORT), in which one object may be relocated at a time, and an object can only be moved if other objects do not block its top surface. In addition, any intermediate structure during the reconfiguration process must be physically stable, i.e., it should stand without external support. To tackle the dual challenges of untangling the dependencies between objects and ensuring structural stability, we develop an algorithm that interleaves the computation of the optimal rearrangement plan and structural stability checking. Using a carefully constructed integer linear programming (ILP) model, our algorithm, Stability-aware Integer Programming-based Planner (SIPP), readily scales to optimally solve complex rearrangement problems of 3D structures with over 60 building blocks, with solution quality significantly outperforming natural greedy best-first approaches. Upon the publication of the manuscript, source code and data will be available at https://github.com/arc-l/mort/

Minimizing Running Buffers for Tabletop Object Rearrangement: Complexity, Fast Algorithms, and Applications

For rearranging objects on tabletops with overhand grasps, temporarily relocating objects to some buffer space may be necessary. This raises the natural question of how many simultaneous storage spaces, or "running buffers", are required so that certain classes of tabletop rearrangement problems are feasible. In this work, we examine the problem for both labeled and unlabeled settings. On the structural side, we observe that finding the minimum number of running buffers (MRB) can be carried out on a dependency graph abstracted from a problem instance, and show that computing MRB is NP-hard. We then prove that under both labeled and unlabeled settings, even for uniform cylindrical objects, the number of required running buffers may grow unbounded as the number of objects to be rearranged increases. We further show that the bound for the unlabeled case is tight. On the algorithmic side, we develop effective exact algorithms for finding MRB for both labeled and unlabeled tabletop rearrangement problems, scalable to over a hundred objects under very high object density. More importantly, our algorithms also compute a sequence witnessing the computed MRB that can be used for solving object rearrangement tasks. Employing these algorithms, empirical evaluations reveal that random labeled and unlabeled instances, which more closely mimics real-world setups, generally have fairly small MRBs. Using real robot experiments, we demonstrate that the running buffer abstraction leads to state-of-the-art solutions for in-place rearrangement of many objects in tight, bounded workspace.

Efficient Algorithms for Boundary Defense with Heterogeneous Defenders

This paper studies the problem of defending (1D and 2D) boundaries against a large number of continuous attacks with a heterogeneous group of defenders. The defender team has perfect information of the attack events within some time (finite or infinite) horizon, with the goal of intercepting as many attacks as possible. An attack is considered successfully intercepted if a defender is present at the boundary location when and where the attack happens. Through proposing a network-flow and integer programming-based method for computing optimal solutions, and an exhaustive defender pairing heuristic method for computing near-optimal solutions, we are able to significantly reduce the computation burden in solving the problem in comparison to the previous state of the art. Extensive simulation experiments confirm the effectiveness of the algorithms. Leveraging our efficient methods, we also characterize the solution structures, revealing the relationships between the attack interception rate and the various problem parameters, e.g., the heterogeneity of the defenders, attack rate, boundary topology, and the look-ahead horizon.

Optimal Allocation of Many Robot Guards for Sweep-Line Coverage

We study the problem of allocating many mobile robots for the execution of a pre-defined sweep schedule in a known two-dimensional environment, with applications toward search and rescue, coverage, surveillance, monitoring, pursuit-evasion, and so on. The mobile robots (or agents) are assumed to have one-dimensional sensing capability with probabilistic guarantees that deteriorate as the sensing distance increases. In solving such tasks, a time-parameterized distribution of robots along the sweep frontier must be computed, with the objective to minimize the number of robots used to achieve some desired coverage quality guarantee or to maximize the probabilistic guarantee for a given number of robots. We propose a max-flow based algorithm for solving the allocation task, which builds on a decomposition technique of the workspace as a generalization of the well-known boustrophedon decomposition. Our proposed algorithm has a very low polynomial running time and completes in under two seconds for polygonal environments with over $10^5$ vertices. Simulation experiments are carried out on three realistic use cases with randomly generated obstacles of varying shapes, sizes, and spatial distributions, which demonstrate the applicability and scalability our proposed method.

Barrier Forming: Separating Polygonal Sets with Minimum Number of Lines

In this work, we carry out structural and algorithmic studies of a problem of barrier forming: selecting theminimum number of straight line segments (barriers) that separate several sets of mutually disjoint objects in the plane. The problem models the optimal placement of line sensors (e.g., infrared laser beams) for isolating many types of regions in a pair-wise manner for practical purposes (e.g., guarding against intrusions). The problem is NP-hard even if we want to find the minimum number of lines to separate two sets of points in the plane. Under the umbrella problem of barrier forming with minimum number of line segments, three settings are examined: barrier forming for point sets, point sets with polygonal obstacles, polygonal sets with polygonal obstacles. We describe methods for computing the optimal solution for the first two settings with the assistance of mathematical programming, and provide a 2-OPT solution for the third. We demonstrate the effectiveness of our methods through extensive simulations.

On Minimizing the Number of Running Buffers for Tabletop Rearrangement

For tabletop rearrangement problems with overhand grasps, storage space outside the tabletop workspace, or buffers, can temporarily hold objects which greatly facilitates the resolution of a given rearrangement task. This brings forth the natural question of how many running buffers are required so that certain classes of tabletop rearrangement problems are feasible. In this work, we examine the problem for both the labeled (where each object has a specific goal pose) and the unlabeled (where goal poses of objects are interchangeable) settings. On the structural side, we observe that finding the minimum number of running buffers (MRB) can be carried out on a dependency graph abstracted from a problem instance, and show that computing MRB on dependency graphs is NP-hard. We then prove that under both labeled and unlabeled settings, even for uniform cylindrical objects, the number of required running buffers may grow unbounded as the number of objects to be rearranged increases; we further show that the bound for the unlabeled case is tight. On the algorithmic side, we develop highly effective algorithms for finding MRB for both labeled and unlabeled tabletop rearrangement problems, scalable to over a hundred objects under very high object density. Employing these algorithms, empirical evaluations show that random labeled and unlabeled instances, which more closely mimics real-world setups, have much smaller MRBs.

Sensor Placement for Globally Optimal Coverage of 3D-Embedded Surfaces

We carry out a structural and algorithmic study of a mobile sensor coverage optimization problem targeting 2D surfaces embedded in a 3D workspace. The investigated settings model multiple important applications including camera network deployment for surveillance, geological monitoring/survey of 3D terrains, and UVC-based surface disinfection for the prevention of the spread of disease agents (e.g., SARS-CoV-2). Under a unified general "sensor coverage" problem, three concrete formulations are examined, focusing on optimizing visibility, single-best coverage quality, and cumulative quality, respectively. After demonstrating the computational intractability of all these formulations, we describe approximation schemes and mathematical programming models for near-optimally solving them. The effectiveness of our methods is thoroughly evaluated under realistic and practical scenarios.

Optimally Guarding Perimeters and Regions with Mobile Range Sensors

We investigate the problem of using mobile robots equipped with 2D range sensors to optimally guard perimeters or regions, i.e., 1D or 2D sets. Given such a set of arbitrary shape to be guarded, and $k$ mobile sensors where the $i$-th sensor can guard a circular region with a variable radius $r_i$, we seek the optimal strategy to deploy the $k$ sensors to fully cover the set such that $\max r_i$ is minimized. On the side of computational complexity, we show that computing a $1.152$-optimal solution for guarding a perimeter or a region is NP-hard, i.e., the problem is hard to approximate. The hardness result on perimeter guarding holds when each sensor may guard at most two disjoint perimeter segments. On the side of computational methods, for the guarding perimeters, we develop a fully polynomial time approximation scheme (FPTAS) for the special setting where each sensor may only guard a single continuous perimeter segment, suggesting that the aforementioned hard-to-approximate result on the two-disjoint-segment sensing model is tight. For the general problem, we first describe a polynomial-time (2+$\epsilon)$-approximation algorithm as an upper bound, applicable to both perimeter guarding and region guarding. This is followed by a high-performance integer linear programming (ILP) based method that computes near-optimal solutions. Thorough computational benchmarks as well as evaluation on potential application scenarios demonstrate the effectiveness of these algorithmic solutions.