Optimal Perimeter Guarding with Heterogeneous Robot Teams: Complexity Analysis and Effective Algorithms
Paper and Code
Dec 17, 2019
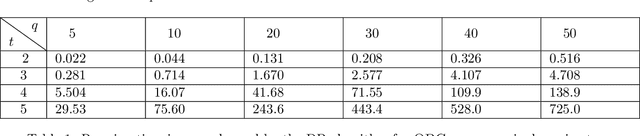


We perform structural and algorithmic studies of significantly generalized versions of the optimal perimeter guarding (OPG) problem. As compared with the original OPG where robots are uniform, in this paper, many mobile robots with heterogeneous sensing capabilities are to be deployed to optimally guard a set of one-dimensional segments. Two complimentary formulations are investigated where one limits the number of available robots (OPG_LR) and the other seeks to minimize the total deployment cost (OPG_MC). In contrast to the original OPG which admits low-polynomial time solutions, both OPG_LR and OPG_MC are computationally intractable with OPG_LR being strongly NP-hard. Nevertheless, we develop fairly scalable pseudo-polynomial time algorithms for practical, fixed-parameter subcase of OPG_LR; we also develop pseudo-polynomial time algorithm for general OPG_MC and polynomial time algorithm for the fixed-parameter OPG_MC case. The applicability and effectiveness of selected algorithms are demonstrated through extensive numerical experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge