Shree Hari Sureshbabu
Prospects of Privacy Advantage in Quantum Machine Learning
May 15, 2024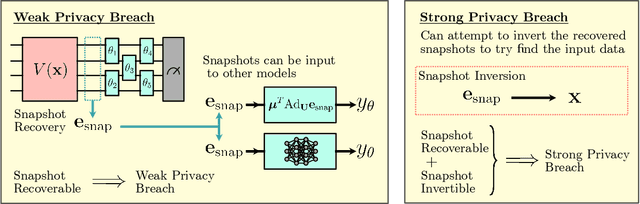
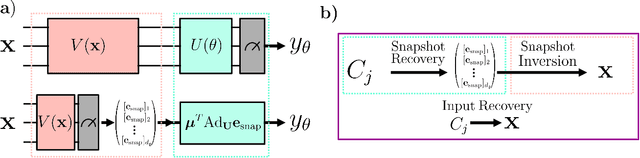
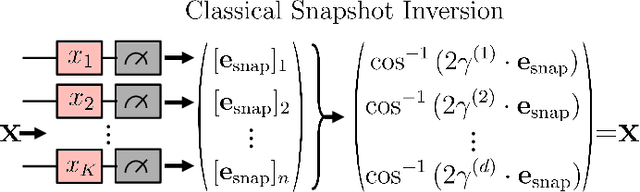
Abstract:Ensuring data privacy in machine learning models is critical, particularly in distributed settings where model gradients are typically shared among multiple parties to allow collaborative learning. Motivated by the increasing success of recovering input data from the gradients of classical models, this study addresses a central question: How hard is it to recover the input data from the gradients of quantum machine learning models? Focusing on variational quantum circuits (VQC) as learning models, we uncover the crucial role played by the dynamical Lie algebra (DLA) of the VQC ansatz in determining privacy vulnerabilities. While the DLA has previously been linked to the classical simulatability and trainability of VQC models, this work, for the first time, establishes its connection to the privacy of VQC models. In particular, we show that properties conducive to the trainability of VQCs, such as a polynomial-sized DLA, also facilitate the extraction of detailed snapshots of the input. We term this a weak privacy breach, as the snapshots enable training VQC models for distinct learning tasks without direct access to the original input. Further, we investigate the conditions for a strong privacy breach where the original input data can be recovered from these snapshots by classical or quantum-assisted polynomial time methods. We establish conditions on the encoding map such as classical simulatability, overlap with DLA basis, and its Fourier frequency characteristics that enable such a privacy breach of VQC models. Our findings thus play a crucial role in detailing the prospects of quantum privacy advantage by guiding the requirements for designing quantum machine learning models that balance trainability with robust privacy protection.
Expressive variational quantum circuits provide inherent privacy in federated learning
Sep 25, 2023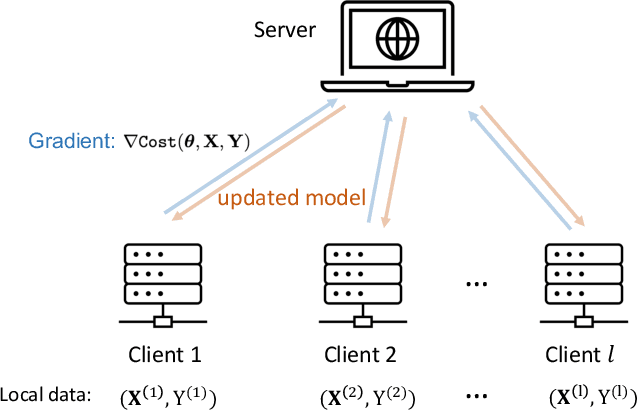
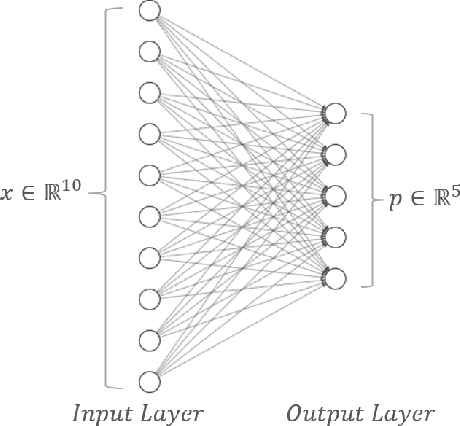
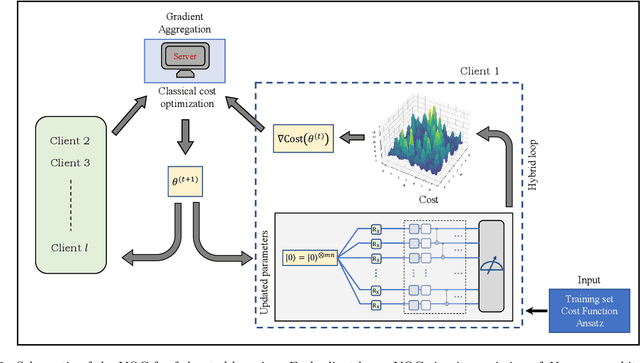
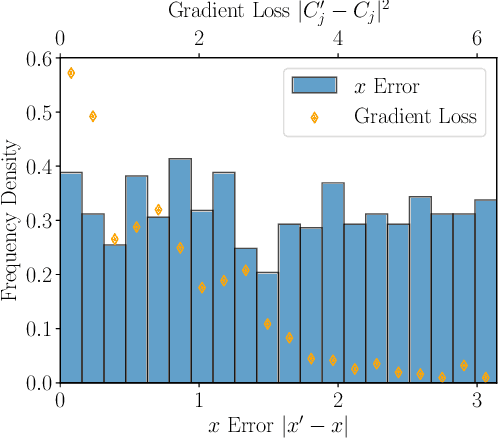
Abstract:Federated learning has emerged as a viable distributed solution to train machine learning models without the actual need to share data with the central aggregator. However, standard neural network-based federated learning models have been shown to be susceptible to data leakage from the gradients shared with the server. In this work, we introduce federated learning with variational quantum circuit model built using expressive encoding maps coupled with overparameterized ans\"atze. We show that expressive maps lead to inherent privacy against gradient inversion attacks, while overparameterization ensures model trainability. Our privacy framework centers on the complexity of solving the system of high-degree multivariate Chebyshev polynomials generated by the gradients of quantum circuit. We present compelling arguments highlighting the inherent difficulty in solving these equations, both in exact and approximate scenarios. Additionally, we delve into machine learning-based attack strategies and establish a direct connection between overparameterization in the original federated learning model and underparameterization in the attack model. Furthermore, we provide numerical scaling arguments showcasing that underparameterization of the expressive map in the attack model leads to the loss landscape being swamped with exponentially many spurious local minima points, thus making it extremely hard to realize a successful attack. This provides a strong claim, for the first time, that the nature of quantum machine learning models inherently helps prevent data leakage in federated learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge