Prospects of Privacy Advantage in Quantum Machine Learning
Paper and Code
May 15, 2024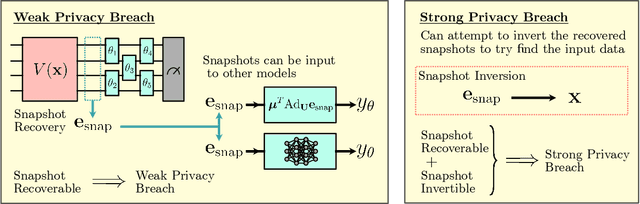
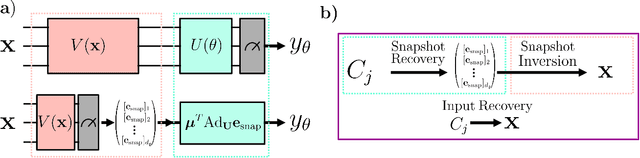
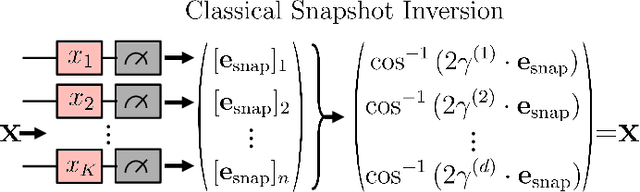
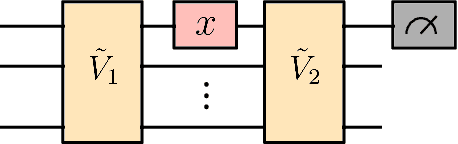
Ensuring data privacy in machine learning models is critical, particularly in distributed settings where model gradients are typically shared among multiple parties to allow collaborative learning. Motivated by the increasing success of recovering input data from the gradients of classical models, this study addresses a central question: How hard is it to recover the input data from the gradients of quantum machine learning models? Focusing on variational quantum circuits (VQC) as learning models, we uncover the crucial role played by the dynamical Lie algebra (DLA) of the VQC ansatz in determining privacy vulnerabilities. While the DLA has previously been linked to the classical simulatability and trainability of VQC models, this work, for the first time, establishes its connection to the privacy of VQC models. In particular, we show that properties conducive to the trainability of VQCs, such as a polynomial-sized DLA, also facilitate the extraction of detailed snapshots of the input. We term this a weak privacy breach, as the snapshots enable training VQC models for distinct learning tasks without direct access to the original input. Further, we investigate the conditions for a strong privacy breach where the original input data can be recovered from these snapshots by classical or quantum-assisted polynomial time methods. We establish conditions on the encoding map such as classical simulatability, overlap with DLA basis, and its Fourier frequency characteristics that enable such a privacy breach of VQC models. Our findings thus play a crucial role in detailing the prospects of quantum privacy advantage by guiding the requirements for designing quantum machine learning models that balance trainability with robust privacy protection.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge