Tracking an Underwater Target with Unknown Measurement Noise Statistics Using Variational Bayesian Filters

This paper considers a bearings-only tracking problem using noisy measurements of unknown noise statistics from a passive sensor. It is assumed that the process and measurement noise follows the Gaussian distribution where the measurement noise has an unknown non-zero mean and unknown covariance. Here an adaptive nonlinear filtering technique is proposed where the joint distribution of the measurement noise mean and its covariance are considered to be following normal inverse Wishart distribution (NIW). Using the variational Bayesian (VB) method the estimation technique is derived with optimized tuning parameters i.e, the confidence parameter and the initial degree of freedom of the measurement noise mean and the covariance, respectively. The proposed filtering technique is compared with the adaptive filtering techniques based on maximum likelihood and maximum aposteriori in terms of root mean square error in position and velocity, bias norm, average normalized estimation error squared, percentage of track loss, and relative execution time. Both adaptive filtering techniques are implemented using the traditional Gaussian approximate filters and are applied to a bearings-only tracking problem illustrated with moderately nonlinear and highly nonlinear scenarios to track a target following a nearly straight line path. Two cases are considered for each scenario, one when the measurement noise covariance is static and another when the measurement noise covariance is varying linearly with the distance between the target and the ownship. In this work, the proposed adaptive filters using the VB approach are found to be superior to their corresponding adaptive filters based on the maximum aposteriori and the maximum likelihood at the expense of higher computation cost.

Risk Sensitive Filtering with Randomly Delayed Measurements

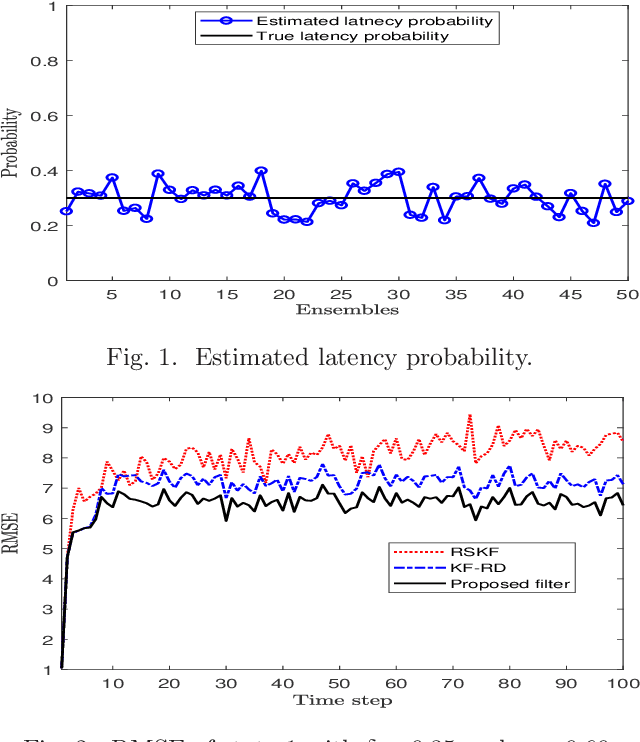
Conventional Bayesian estimation requires an accurate stochastic model of a system. However, this requirement is not always met in many practical cases where the system is not completely known or may differ from the assumed model. For such a system, we consider a scenario where the measurements are transmitted to a remote location using a common communication network and due to which, a delay is introduced while receiving the measurements. The delay that we consider here is random and one step maximum at a given time instant. For such a scenario, this paper develops a robust estimator for a linear Gaussian system by minimizing the risk sensitive error criterion that is defined as an expectation of the accumulated exponential quadratic error. The criteria for the stability of the risk sensitive Kalman filter (RSKF) are derived and the results are used to study the stability of the developed filter. Further, it is assumed that the latency probability related to delay is not known and it is estimated by maximizing the likelihood function. Simulation results suggest that the proposed filter shows acceptable performance under the nominal conditions, and it performs better than the Kalman filter for randomly delayed measurements and the RSKF in presence of both the model uncertainty and random delays.

Modeling and Estimation for Systems with Randomly Delayed Measurements and Packet Dropouts

A networked system often uses a shared communication network to transmit the measurements to a remotely located estimation center. Due to the limited bandwidth of the channel, a delay may appear while receiving the measurements. This delay can be arbitrary step random, and packets are sometimes dropped during transmission as it exceeds a certain permissible number. In this paper, such measurements are modeled with the Poisson distribution, which allows the user to determine the maximum delay the system might suffer. When the measurement delay exceeds the permissible number, the packet dropout happens. Based on the proposed model, we solve the problem by assuming that the prior and posterior densities of states are Gaussian and derive the expression of the estimated state and the error covariance. Later, relaxing the Gaussian assumption for densities, we propose a solution with the help of the sequential Monte Carlo (SMC) approach. The proposed SMC method divides the set of particles into several groups, where each group supports the possibility that the received measurement is delayed by a certain number of steps. The strength of an individual group is determined by the probability of a measurement being delayed with the same number of steps that the group represents. This approach estimates the states and also assesses the amount of delay from the received measurements. Finally, the developed estimators are implemented on two nonlinear estimation problems, and the simulation results are compared. The proposed SMC approach shows better results compared to the designed Gaussian delay filters and existing particle filters with delay.

Robust Maximum Correntropy Kalman Filter

The Kalman filter provides an optimal estimation for a linear system with Gaussian noise. However when the noises are non-Gaussian in nature, its performance deteriorates rapidly. For non-Gaussian noises, maximum correntropy Kalman filter (MCKF) is developed which provides an improved result. But when the system model differs from nominal consideration, the performance of the MCKF degrades. For such cases, we have proposed a new robust filtering technique which maximize a cost function defined by exponential of weighted past and present errors along with the Gaussian kernel function. By solving this cost criteria we have developed prior and posterior mean and covariance matrix propagation equations. By maximizing the correntropy function of error matrix, we have selected the kernel bandwidth value at each time step. Further the conditions for convergence of the proposed algorithm is also derived. Two numerical examples are presented to show the usefulness of the new filtering technique.

Resolving Left-Right Ambiguity During Bearing Only Tracking of an Underwater Target Using Towed Array

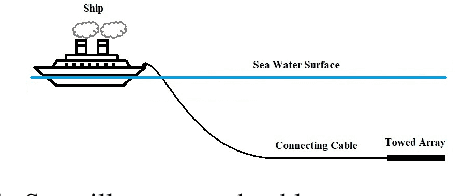
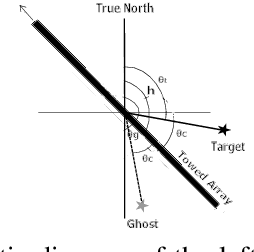
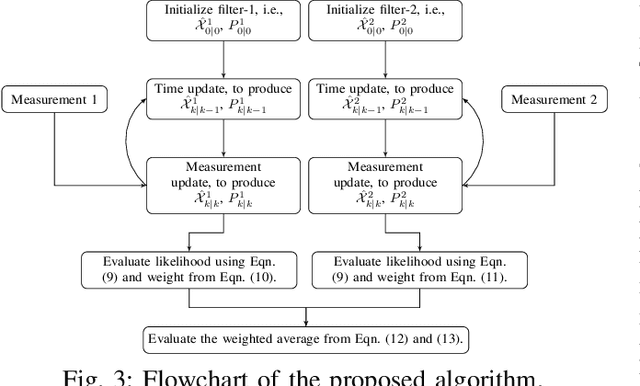
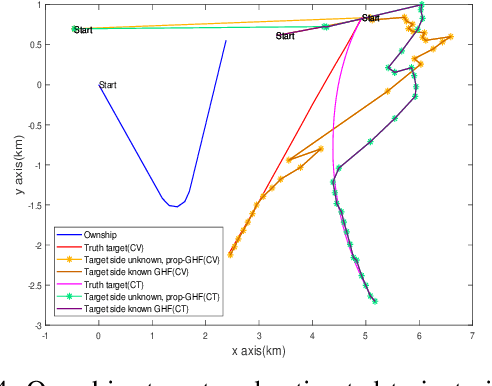
In bearing only tracking using a towed array, the array can sense the bearing angle of the target but is unable to differentiate whether the target is on the left or the right side of the array. Thus, the traditional tracking algorithm generates tracks in both the sides of the array which create difficulties when interception is required. In this paper, we propose a method based on likelihood of measurement which along with the estimators can resolve left-right ambiguity and track the target. A case study has been presented where the target moves (a) in a straight line with a near constant velocity, (b) maneuvers with a turn, and observer takes a `U'-like maneuver. The method along with the various estimators has been applied which successfully resolves the ambiguity and tracks the target. Further, the tracking results are compared in terms of the root mean square error in position and velocity, bias norm, \% of track loss and the relative execution time.