Shobeir Fakhraei
Biomedical Named Entity Recognition via Reference-Set Augmented Bootstrapping
Jun 01, 2019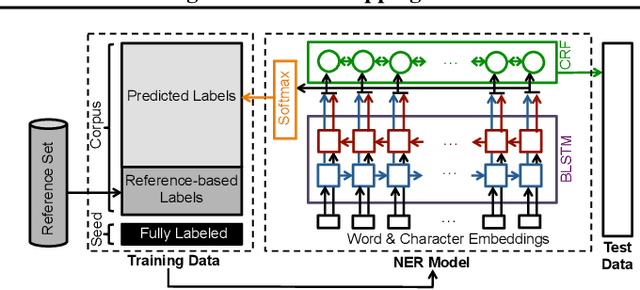
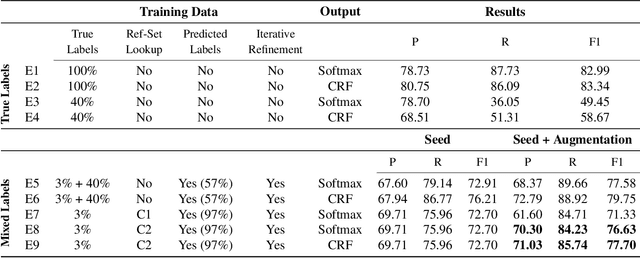
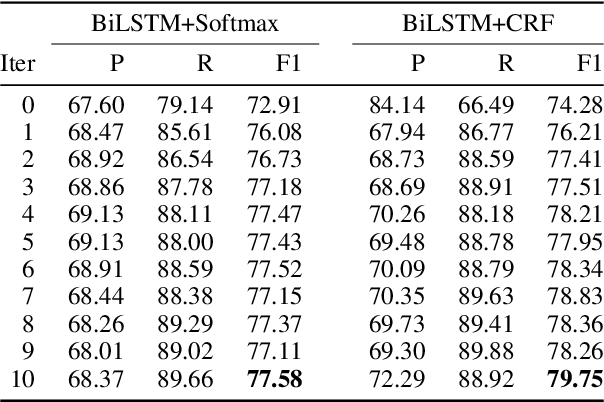
Abstract:We present a weakly-supervised data augmentation approach to improve Named Entity Recognition (NER) in a challenging domain: extracting biomedical entities (e.g., proteins) from the scientific literature. First, we train a neural NER (NNER) model over a small seed of fully-labeled examples. Second, we use a reference set of entity names (e.g., proteins in UniProt) to identify entity mentions with high precision, but low recall, on an unlabeled corpus. Third, we use the NNER model to assign weak labels to the corpus. Finally, we retrain our NNER model iteratively over the augmented training set, including the seed, the reference-set examples, and the weakly-labeled examples, which improves model performance. We show empirically that this augmented bootstrapping process significantly improves NER performance, and discuss the factors impacting the efficacy of the approach.
NSEEN: Neural Semantic Embedding for Entity Normalization
Nov 19, 2018



Abstract:Much of human knowledge is encoded in the text, such as scientific publications, books, and the web. Given the rapid growth of these resources, we need automated methods to extract such knowledge into formal, machine-processable structures, such as knowledge graphs. An important task in this process is entity normalization (also called entity grounding, or resolution), which consists of mapping entity mentions in text to canonical entities in well-known reference sets. However, entity resolution is a challenging problem, since there often are many textual forms for a canonical entity. The problem is particularly acute in the scientific domain, such as biology. For example, a protein may have many different names and syntactic variations on these names. To address this problem, we have developed a general, scalable solution based on a deep Siamese neural network model to embed the semantic information about the entities, as well as their syntactic variations. We use these embeddings for fast mapping of new entities to large reference sets, and empirically show the effectiveness of our framework in challenging bio-entity normalization datasets.
Adaptive Neighborhood Graph Construction for Inference in Multi-Relational Networks
Jul 02, 2016


Abstract:A neighborhood graph, which represents the instances as vertices and their relations as weighted edges, is the basis of many semi-supervised and relational models for node labeling and link prediction. Most methods employ a sequential process to construct the neighborhood graph. This process often consists of generating a candidate graph, pruning the candidate graph to make a neighborhood graph, and then performing inference on the variables (i.e., nodes) in the neighborhood graph. In this paper, we propose a framework that can dynamically adapt the neighborhood graph based on the states of variables from intermediate inference results, as well as structural properties of the relations connecting them. A key strength of our framework is its ability to handle multi-relational data and employ varying amounts of relations for each instance based on the intermediate inference results. We formulate the link prediction task as inference on neighborhood graphs, and include preliminary results illustrating the effects of different strategies in our proposed framework.
Comparing apples to apples in the evaluation of binary coding methods
Sep 27, 2014



Abstract:We discuss methodological issues related to the evaluation of unsupervised binary code construction methods for nearest neighbor search. These issues have been widely ignored in literature. These coding methods attempt to preserve either Euclidean distance or angular (cosine) distance in the binary embedding space. We explain why when comparing a method whose goal is preserving cosine similarity to one designed for preserving Euclidean distance, the original features should be normalized by mapping them to the unit hypersphere before learning the binary mapping functions. To compare a method whose goal is to preserves Euclidean distance to one that preserves cosine similarity, the original feature data must be mapped to a higher dimension by including a bias term in binary mapping functions. These conditions ensure the fair comparison between different binary code methods for the task of nearest neighbor search. Our experiments show under these conditions the very simple methods (e.g. LSH and ITQ) often outperform recent state-of-the-art methods (e.g. MDSH and OK-means).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge