A Peaceman-Rachford Splitting Approach with Deep Equilibrium Network for Channel Estimation

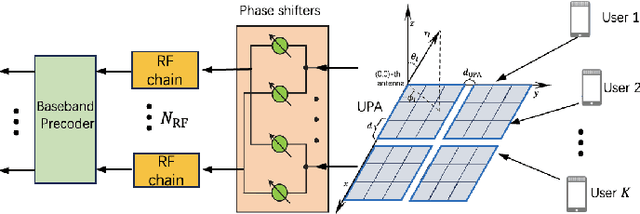
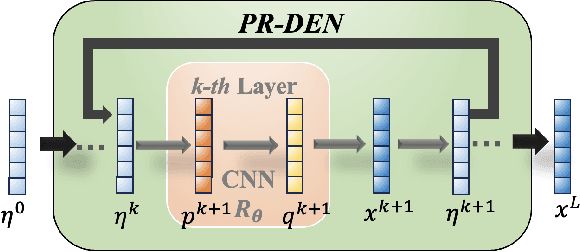
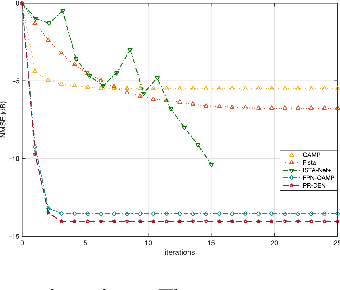
Multiple-input multiple-output (MIMO) is pivotal for wireless systems, yet its high-dimensional, stochastic channel poses significant challenges for accurate estimation, highlighting the critical need for robust estimation techniques. In this paper, we introduce a novel channel estimation method for the MIMO system. The main idea is to construct a fixed-point equation for channel estimation, which can be implemented into the deep equilibrium (DEQ) model with a fixed network. Specifically, the Peaceman-Rachford (PR) splitting method is applied to the dual form of the regularized minimization problem to construct fixed-point equation with non-expansive property. Then, the fixed-point equation is implemented into the DEQ model with a fixed layer, leveraging its advantage of the low training complexity. Moreover, we provide a rigorous theoretical analysis, demonstrating the convergence and optimality of our approach. Additionally, simulations of hybrid far- and near-field channels demonstrate that our approach yields favorable results, indicating its ability to advance channel estimation in MIMO system.

Variations on a Theme by Blahut and Arimoto

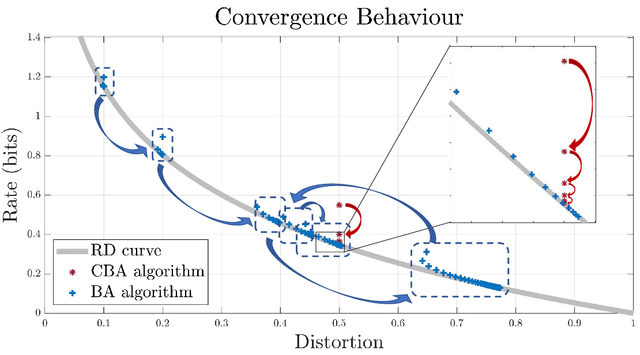
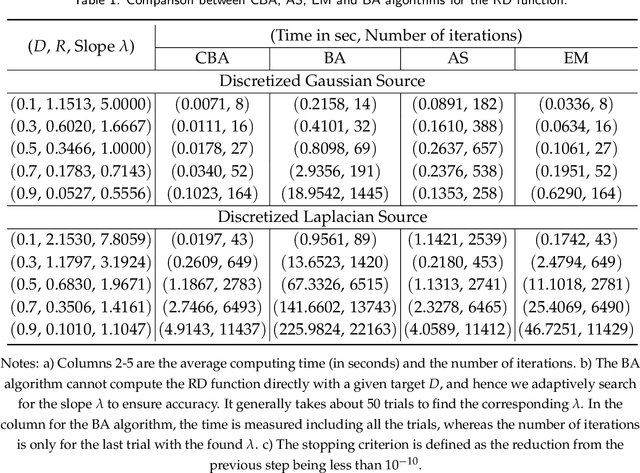
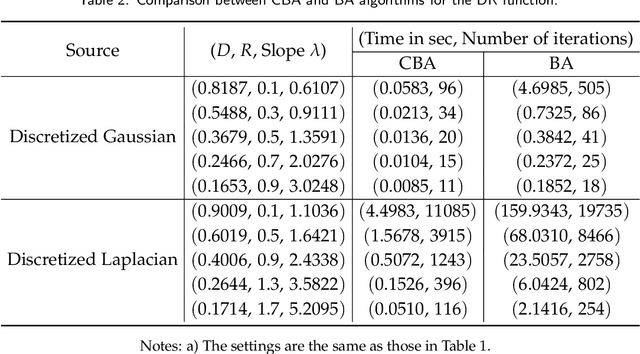
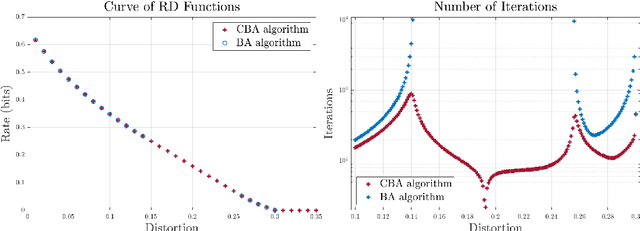
The Blahut-Arimoto (BA) algorithm has played a fundamental role in the numerical computation of rate-distortion (RD) functions. This algorithm possesses a desirable monotonic convergence property by alternatively minimizing its Lagrangian with a fixed multiplier. In this paper, we propose a novel modification of the BA algorithm, letting the multiplier be updated in each iteration via a one-dimensional root-finding step with respect to a monotonic univariate function, which can be efficiently implemented by Newton's method. This allows the multiplier to be updated in a flexible and efficient manner, overcoming a major drawback of the original BA algorithm wherein the multiplier is fixed throughout iterations. Consequently, the modified algorithm is capable of directly computing the RD function for a given target distortion, without exploring the entire RD curve as in the original BA algorithm. A theoretical analysis shows that the modified algorithm still converges to the RD function and the convergence rate is $\Theta(1/n)$, where $n$ denotes the number of iterations. Numerical experiments demonstrate that the modified algorithm directly computes the RD function with a given target distortion, and it significantly accelerates the original BA algorithm.