Variations on a Theme by Blahut and Arimoto
Paper and Code
May 04, 2023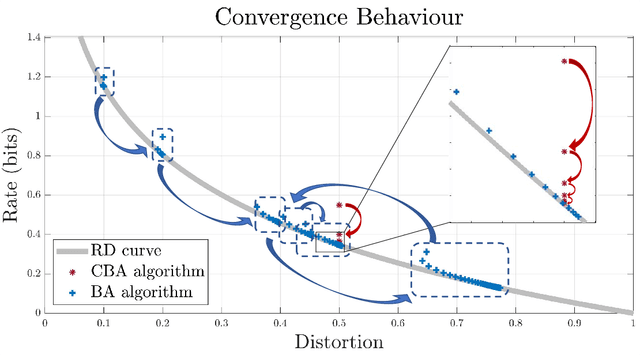
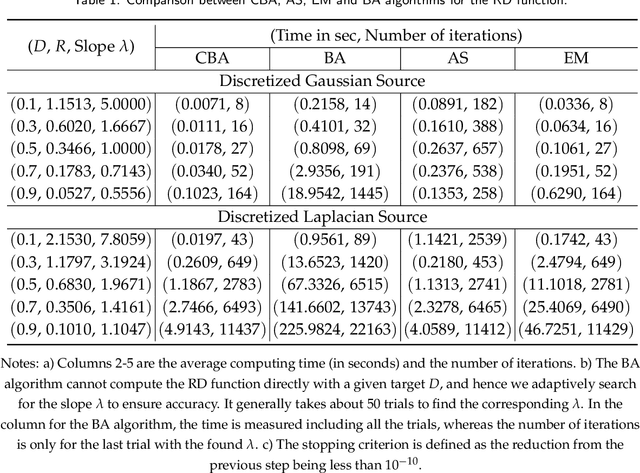
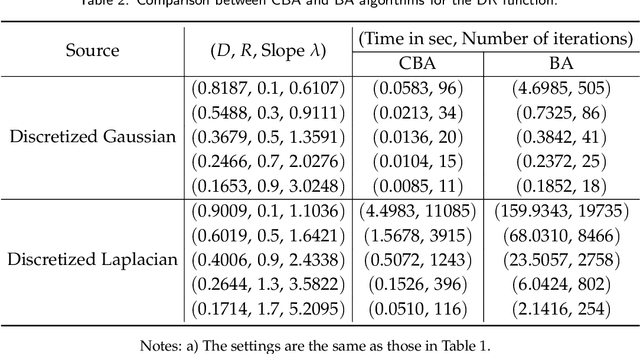
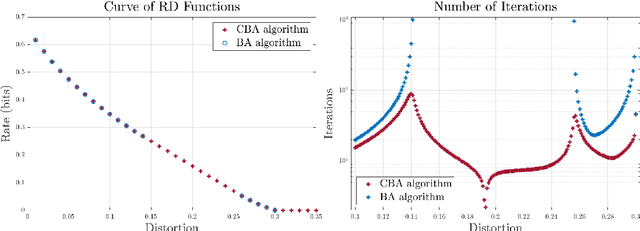
The Blahut-Arimoto (BA) algorithm has played a fundamental role in the numerical computation of rate-distortion (RD) functions. This algorithm possesses a desirable monotonic convergence property by alternatively minimizing its Lagrangian with a fixed multiplier. In this paper, we propose a novel modification of the BA algorithm, letting the multiplier be updated in each iteration via a one-dimensional root-finding step with respect to a monotonic univariate function, which can be efficiently implemented by Newton's method. This allows the multiplier to be updated in a flexible and efficient manner, overcoming a major drawback of the original BA algorithm wherein the multiplier is fixed throughout iterations. Consequently, the modified algorithm is capable of directly computing the RD function for a given target distortion, without exploring the entire RD curve as in the original BA algorithm. A theoretical analysis shows that the modified algorithm still converges to the RD function and the convergence rate is $\Theta(1/n)$, where $n$ denotes the number of iterations. Numerical experiments demonstrate that the modified algorithm directly computes the RD function with a given target distortion, and it significantly accelerates the original BA algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge