Shaocong Ma
Riemannian Zeroth-Order Gradient Estimation with Structure-Preserving Metrics for Geodesically Incomplete Manifolds
Jan 12, 2026Abstract:In this paper, we study Riemannian zeroth-order optimization in settings where the underlying Riemannian metric $g$ is geodesically incomplete, and the goal is to approximate stationary points with respect to this incomplete metric. To address this challenge, we construct structure-preserving metrics that are geodesically complete while ensuring that every stationary point under the new metric remains stationary under the original one. Building on this foundation, we revisit the classical symmetric two-point zeroth-order estimator and analyze its mean-squared error from a purely intrinsic perspective, depending only on the manifold's geometry rather than any ambient embedding. Leveraging this intrinsic analysis, we establish convergence guarantees for stochastic gradient descent with this intrinsic estimator. Under additional suitable conditions, an $ε$-stationary point under the constructed metric $g'$ also corresponds to an $ε$-stationary point under the original metric $g$, thereby matching the best-known complexity in the geodesically complete setting. Empirical studies on synthetic problems confirm our theoretical findings, and experiments on a practical mesh optimization task demonstrate that our framework maintains stable convergence even in the absence of geodesic completeness.
Rectified Robust Policy Optimization for Model-Uncertain Constrained Reinforcement Learning without Strong Duality
Aug 24, 2025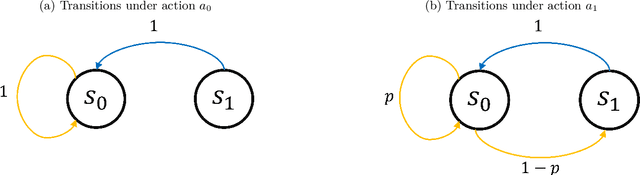
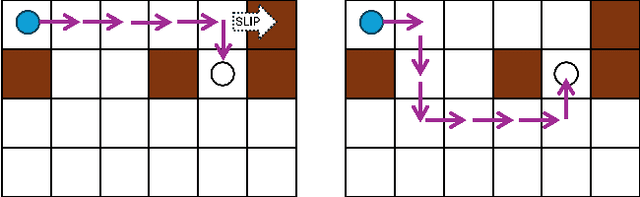
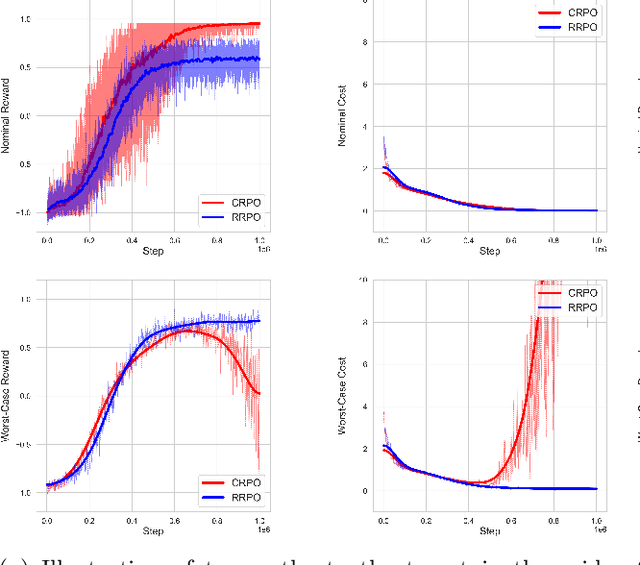
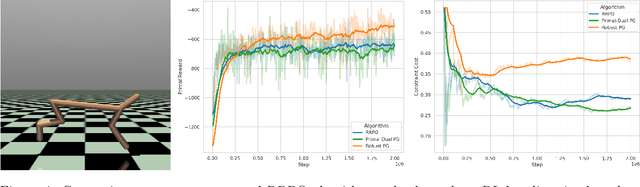
Abstract:The goal of robust constrained reinforcement learning (RL) is to optimize an agent's performance under the worst-case model uncertainty while satisfying safety or resource constraints. In this paper, we demonstrate that strong duality does not generally hold in robust constrained RL, indicating that traditional primal-dual methods may fail to find optimal feasible policies. To overcome this limitation, we propose a novel primal-only algorithm called Rectified Robust Policy Optimization (RRPO), which operates directly on the primal problem without relying on dual formulations. We provide theoretical convergence guarantees under mild regularity assumptions, showing convergence to an approximately optimal feasible policy with iteration complexity matching the best-known lower bound when the uncertainty set diameter is controlled in a specific level. Empirical results in a grid-world environment validate the effectiveness of our approach, demonstrating that RRPO achieves robust and safe performance under model uncertainties while the non-robust method can violate the worst-case safety constraints.
End-to-End Mesh Optimization of a Hybrid Deep Learning Black-Box PDE Solver
Apr 17, 2024



Abstract:Deep learning has been widely applied to solve partial differential equations (PDEs) in computational fluid dynamics. Recent research proposed a PDE correction framework that leverages deep learning to correct the solution obtained by a PDE solver on a coarse mesh. However, end-to-end training of such a PDE correction model over both solver-dependent parameters such as mesh parameters and neural network parameters requires the PDE solver to support automatic differentiation through the iterative numerical process. Such a feature is not readily available in many existing solvers. In this study, we explore the feasibility of end-to-end training of a hybrid model with a black-box PDE solver and a deep learning model for fluid flow prediction. Specifically, we investigate a hybrid model that integrates a black-box PDE solver into a differentiable deep graph neural network. To train this model, we use a zeroth-order gradient estimator to differentiate the PDE solver via forward propagation. Although experiments show that the proposed approach based on zeroth-order gradient estimation underperforms the baseline that computes exact derivatives using automatic differentiation, our proposed method outperforms the baseline trained with a frozen input mesh to the solver. Moreover, with a simple warm-start on the neural network parameters, we show that models trained by these zeroth-order algorithms achieve an accelerated convergence and improved generalization performance.
Data Sampling Affects the Complexity of Online SGD over Dependent Data
Mar 31, 2022
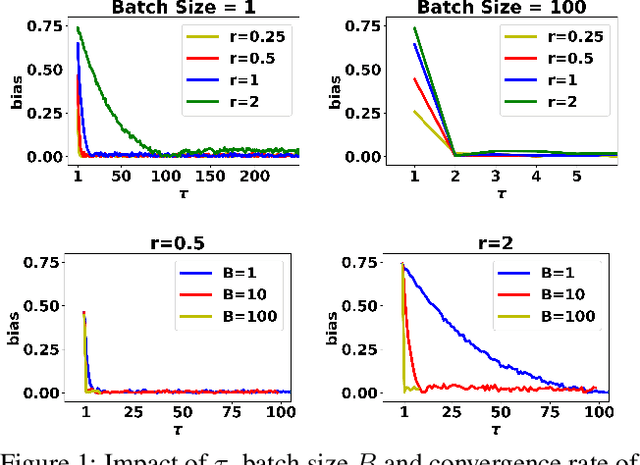
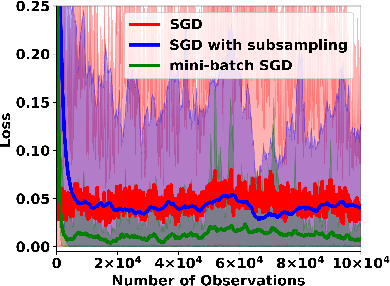
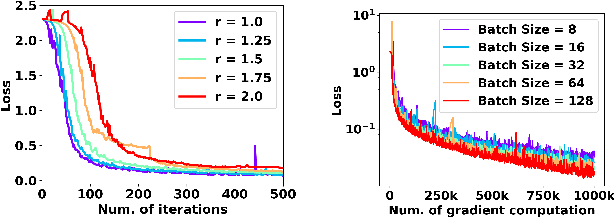
Abstract:Conventional machine learning applications typically assume that data samples are independently and identically distributed (i.i.d.). However, practical scenarios often involve a data-generating process that produces highly dependent data samples, which are known to heavily bias the stochastic optimization process and slow down the convergence of learning. In this paper, we conduct a fundamental study on how different stochastic data sampling schemes affect the sample complexity of online stochastic gradient descent (SGD) over highly dependent data. Specifically, with a $\phi$-mixing model of data dependence, we show that online SGD with proper periodic data-subsampling achieves an improved sample complexity over the standard online SGD in the full spectrum of the data dependence level. Interestingly, even subsampling a subset of data samples can accelerate the convergence of online SGD over highly dependent data. Moreover, we show that online SGD with mini-batch sampling can further substantially improve the sample complexity over online SGD with periodic data-subsampling over highly dependent data. Numerical experiments validate our theoretical results.
Accelerated Proximal Alternating Gradient-Descent-Ascent for Nonconvex Minimax Machine Learning
Dec 30, 2021

Abstract:Alternating gradient-descent-ascent (AltGDA) is an optimization algorithm that has been widely used for model training in various machine learning applications, which aim to solve a nonconvex minimax optimization problem. However, the existing studies show that it suffers from a high computation complexity in nonconvex minimax optimization. In this paper, we develop a single-loop and fast AltGDA-type algorithm that leverages proximal gradient updates and momentum acceleration to solve regularized nonconvex minimax optimization problems. By identifying the intrinsic Lyapunov function of this algorithm, we prove that it converges to a critical point of the nonconvex minimax optimization problem and achieves a computation complexity $\mathcal{O}(\kappa^{1.5}\epsilon^{-2})$, where $\epsilon$ is the desired level of accuracy and $\kappa$ is the problem's condition number. Such a computation complexity improves the state-of-the-art complexities of single-loop GDA and AltGDA algorithms (see the summary of comparison in Table 1). We demonstrate the effectiveness of our algorithm via an experiment on adversarial deep learning.
Greedy-GQ with Variance Reduction: Finite-time Analysis and Improved Complexity
Mar 30, 2021



Abstract:Greedy-GQ is a value-based reinforcement learning (RL) algorithm for optimal control. Recently, the finite-time analysis of Greedy-GQ has been developed under linear function approximation and Markovian sampling, and the algorithm is shown to achieve an $\epsilon$-stationary point with a sample complexity in the order of $\mathcal{O}(\epsilon^{-3})$. Such a high sample complexity is due to the large variance induced by the Markovian samples. In this paper, we propose a variance-reduced Greedy-GQ (VR-Greedy-GQ) algorithm for off-policy optimal control. In particular, the algorithm applies the SVRG-based variance reduction scheme to reduce the stochastic variance of the two time-scale updates. We study the finite-time convergence of VR-Greedy-GQ under linear function approximation and Markovian sampling and show that the algorithm achieves a much smaller bias and variance error than the original Greedy-GQ. In particular, we prove that VR-Greedy-GQ achieves an improved sample complexity that is in the order of $\mathcal{O}(\epsilon^{-2})$. We further compare the performance of VR-Greedy-GQ with that of Greedy-GQ in various RL experiments to corroborate our theoretical findings.
Variance-Reduced Off-Policy TDC Learning: Non-Asymptotic Convergence Analysis
Oct 31, 2020


Abstract:Variance reduction techniques have been successfully applied to temporal-difference (TD) learning and help to improve the sample complexity in policy evaluation. However, the existing work applied variance reduction to either the less popular one time-scale TD algorithm or the two time-scale GTD algorithm but with a finite number of i.i.d.\ samples, and both algorithms apply to only the on-policy setting. In this work, we develop a variance reduction scheme for the two time-scale TDC algorithm in the off-policy setting and analyze its non-asymptotic convergence rate over both i.i.d.\ and Markovian samples. In the i.i.d.\ setting, our algorithm achieves a sample complexity $O(\epsilon^{-\frac{3}{5}} \log{\epsilon}^{-1})$ that is lower than the state-of-the-art result $O(\epsilon^{-1} \log {\epsilon}^{-1})$. In the Markovian setting, our algorithm achieves the state-of-the-art sample complexity $O(\epsilon^{-1} \log {\epsilon}^{-1})$ that is near-optimal. Experiments demonstrate that the proposed variance-reduced TDC achieves a smaller asymptotic convergence error than both the conventional TDC and the variance-reduced TD.
Understanding the Impact of Model Incoherence on Convergence of Incremental SGD with Random Reshuffle
Jul 07, 2020



Abstract:Although SGD with random reshuffle has been widely-used in machine learning applications, there is a limited understanding of how model characteristics affect the convergence of the algorithm. In this work, we introduce model incoherence to characterize the diversity of model characteristics and study its impact on convergence of SGD with random reshuffle under weak strong convexity. Specifically, minimizer incoherence measures the discrepancy between the global minimizers of a sample loss and those of the total loss and affects the convergence error of SGD with random reshuffle. In particular, we show that the variable sequence generated by SGD with random reshuffle converges to a certain global minimizer of the total loss under full minimizer coherence. The other curvature incoherence measures the quality of condition numbers of the sample losses and determines the convergence rate of SGD. With model incoherence, our results show that SGD has a faster convergence rate and smaller convergence error under random reshuffle than those under random sampling, and hence provide justifications to the superior practical performance of SGD with random reshuffle.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge