Data Sampling Affects the Complexity of Online SGD over Dependent Data
Paper and Code
Mar 31, 2022
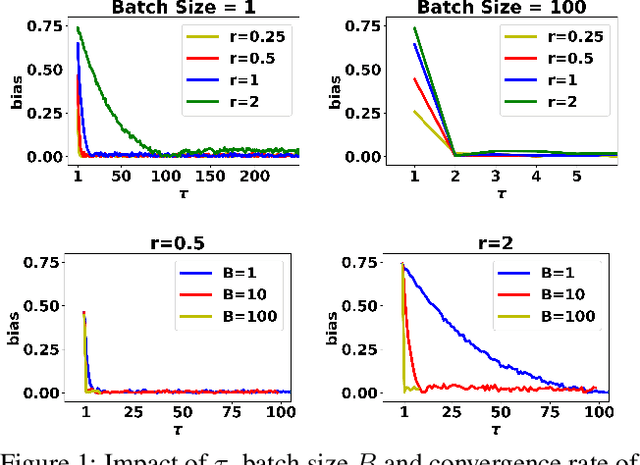
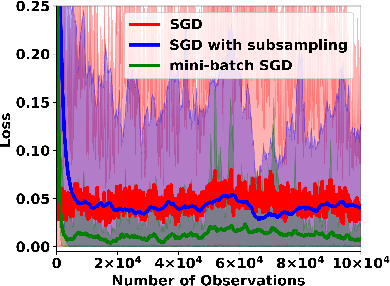
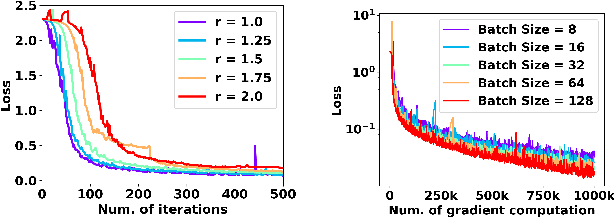
Conventional machine learning applications typically assume that data samples are independently and identically distributed (i.i.d.). However, practical scenarios often involve a data-generating process that produces highly dependent data samples, which are known to heavily bias the stochastic optimization process and slow down the convergence of learning. In this paper, we conduct a fundamental study on how different stochastic data sampling schemes affect the sample complexity of online stochastic gradient descent (SGD) over highly dependent data. Specifically, with a $\phi$-mixing model of data dependence, we show that online SGD with proper periodic data-subsampling achieves an improved sample complexity over the standard online SGD in the full spectrum of the data dependence level. Interestingly, even subsampling a subset of data samples can accelerate the convergence of online SGD over highly dependent data. Moreover, we show that online SGD with mini-batch sampling can further substantially improve the sample complexity over online SGD with periodic data-subsampling over highly dependent data. Numerical experiments validate our theoretical results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge