Shantanu Rane
Zero-Query Transfer Attacks on Context-Aware Object Detectors
Mar 29, 2022

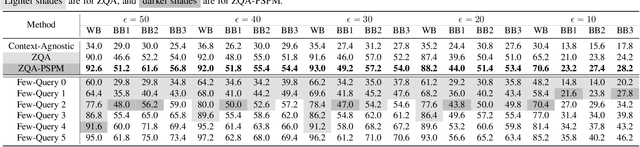

Abstract:Adversarial attacks perturb images such that a deep neural network produces incorrect classification results. A promising approach to defend against adversarial attacks on natural multi-object scenes is to impose a context-consistency check, wherein, if the detected objects are not consistent with an appropriately defined context, then an attack is suspected. Stronger attacks are needed to fool such context-aware detectors. We present the first approach for generating context-consistent adversarial attacks that can evade the context-consistency check of black-box object detectors operating on complex, natural scenes. Unlike many black-box attacks that perform repeated attempts and open themselves to detection, we assume a "zero-query" setting, where the attacker has no knowledge of the classification decisions of the victim system. First, we derive multiple attack plans that assign incorrect labels to victim objects in a context-consistent manner. Then we design and use a novel data structure that we call the perturbation success probability matrix, which enables us to filter the attack plans and choose the one most likely to succeed. This final attack plan is implemented using a perturbation-bounded adversarial attack algorithm. We compare our zero-query attack against a few-query scheme that repeatedly checks if the victim system is fooled. We also compare against state-of-the-art context-agnostic attacks. Against a context-aware defense, the fooling rate of our zero-query approach is significantly higher than context-agnostic approaches and higher than that achievable with up to three rounds of the few-query scheme.
Matrix Factorization-Based Clustering Of Image Features For Bandwidth-Constrained Information Retrieval
May 07, 2016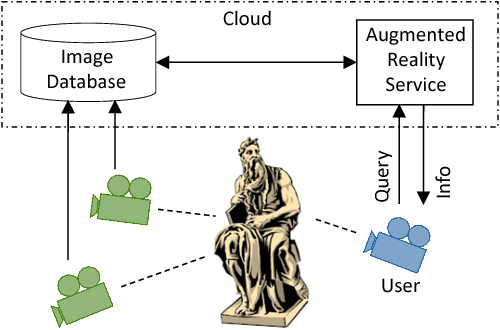

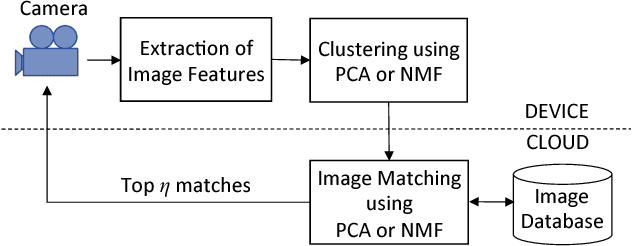

Abstract:We consider the problem of accurately and efficiently querying a remote server to retrieve information about images captured by a mobile device. In addition to reduced transmission overhead and computational complexity, the retrieval protocol should be robust to variations in the image acquisition process, such as translation, rotation, scaling, and sensor-related differences. We propose to extract scale-invariant image features and then perform clustering to reduce the number of features needed for image matching. Principal Component Analysis (PCA) and Non-negative Matrix Factorization (NMF) are investigated as candidate clustering approaches. The image matching complexity at the database server is quadratic in the (small) number of clusters, not in the (very large) number of image features. We employ an image-dependent information content metric to approximate the model order, i.e., the number of clusters, needed for accurate matching, which is preferable to setting the model order using trial and error. We show how to combine the hypotheses provided by PCA and NMF factor loadings, thereby obtaining more accurate retrieval than using either approach alone. In experiments on a database of urban images, we obtain a top-1 retrieval accuracy of 89% and a top-3 accuracy of 92.5%.
Representation and Coding of Signal Geometry
Dec 23, 2015



Abstract:Approaches to signal representation and coding theory have traditionally focused on how to best represent signals using parsimonious representations that incur the lowest possible distortion. Classical examples include linear and non-linear approximations, sparse representations, and rate-distortion theory. Very often, however, the goal of processing is to extract specific information from the signal, and the distortion should be measured on the extracted information. The corresponding representation should, therefore, represent that information as parsimoniously as possible, without necessarily accurately representing the signal itself. In this paper, we examine the problem of encoding signals such that sufficient information is preserved about their pairwise distances and their inner products. For that goal, we consider randomized embeddings as an encoding mechanism and provide a framework to analyze their performance. We also demonstrate that it is possible to design the embedding such that it represents different ranges of distances with different precision. These embeddings also allow the computation of kernel inner products with control on their inner product-preserving properties. Our results provide a broad framework to design and analyze embeddins, and generalize existing results in this area, such as random Fourier kernels and universal embeddings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge