Inferring Tweedie Compound Poisson Mixed Models with Adversarial Variational Bayes

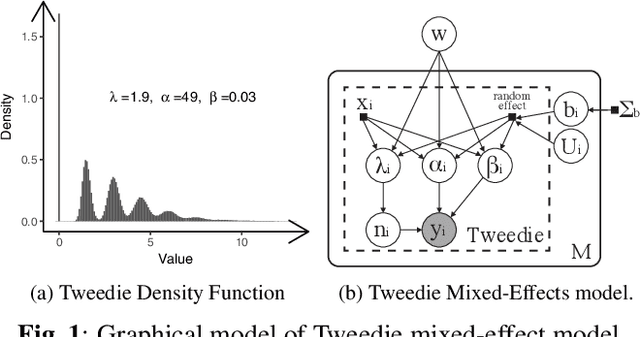
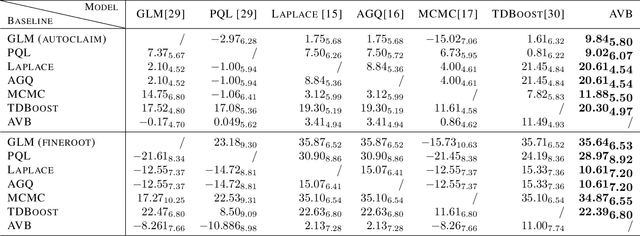
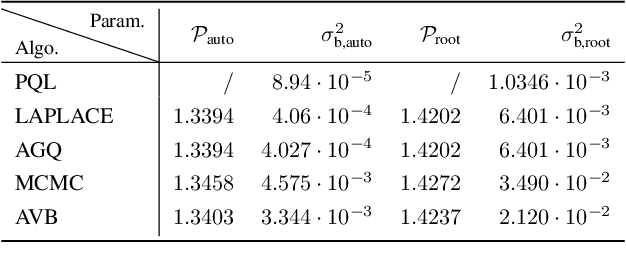
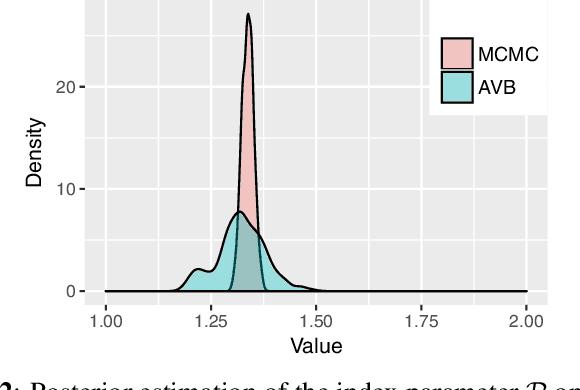
The Tweedie Compound Poisson-Gamma model is routinely used for modelling non-negative continuous data with a discrete probability mass at zero. Mixed models with random effects account for the covariance structure related to the grouping hierarchy in the data. An important application of Tweedie mixed models is estimating the aggregated loss for insurance policies. However, the intractable likelihood function, the unknown variance function, and the hierarchical structure of mixed effects have presented considerable challenges for drawing inferences on Tweedie. In this study, we tackle the Bayesian Tweedie mixed-effects models via variational approaches. In particular, we empower the posterior approximation by implicit models trained in an adversarial setting. To reduce the variance of gradients, we reparameterize random effects, and integrate out one local latent variable of Tweedie. We also employ a flexible hyper prior to ensure the richness of the approximation. Our method is evaluated on both simulated and real-world data. Results show that the proposed method has smaller estimation bias on the random effects compared to traditional inference methods including MCMC; it also achieves a state-of-the-art predictive performance, meanwhile offering a richer estimation of the variance function.

Generative OpenMax for Multi-Class Open Set Classification

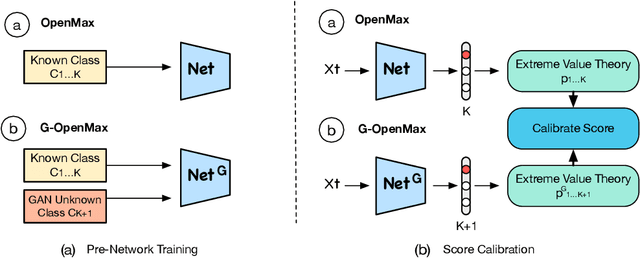
We present a conceptually new and flexible method for multi-class open set classification. Unlike previous methods where unknown classes are inferred with respect to the feature or decision distance to the known classes, our approach is able to provide explicit modelling and decision score for unknown classes. The proposed method, called Gener- ative OpenMax (G-OpenMax), extends OpenMax by employing generative adversarial networks (GANs) for novel category image synthesis. We validate the proposed method on two datasets of handwritten digits and characters, resulting in superior results over previous deep learning based method OpenMax Moreover, G-OpenMax provides a way to visualize samples representing the unknown classes from open space. Our simple and effective approach could serve as a new direction to tackle the challenging multi-class open set classification problem.

Invariant backpropagation: how to train a transformation-invariant neural network

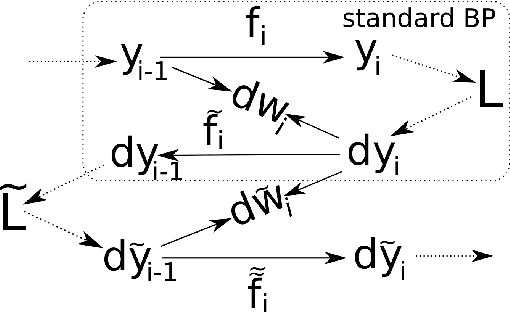
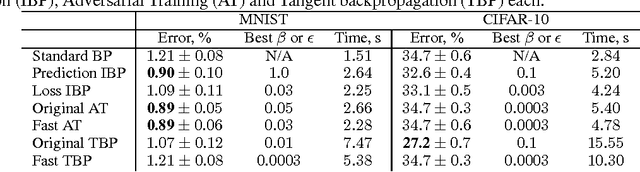
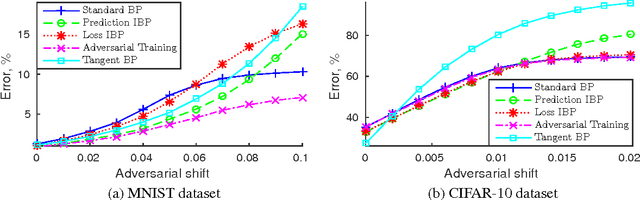
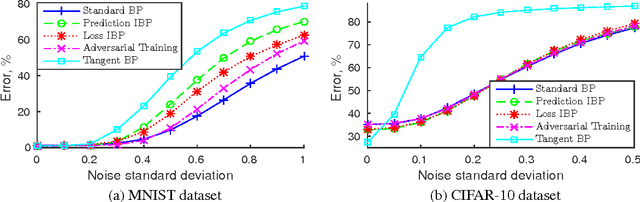
In many classification problems a classifier should be robust to small variations in the input vector. This is a desired property not only for particular transformations, such as translation and rotation in image classification problems, but also for all others for which the change is small enough to retain the object perceptually indistinguishable. We propose two extensions of the backpropagation algorithm that train a neural network to be robust to variations in the feature vector. While the first of them enforces robustness of the loss function to all variations, the second method trains the predictions to be robust to a particular variation which changes the loss function the most. The second methods demonstrates better results, but is slightly slower. We analytically compare the proposed algorithm with two the most similar approaches (Tangent BP and Adversarial Training), and propose their fast versions. In the experimental part we perform comparison of all algorithms in terms of classification accuracy and robustness to noise on MNIST and CIFAR-10 datasets. Additionally we analyze how the performance of the proposed algorithm depends on the dataset size and data augmentation.