Invariant backpropagation: how to train a transformation-invariant neural network
Paper and Code
Jan 15, 2016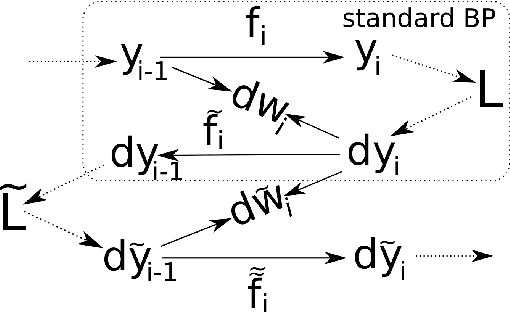
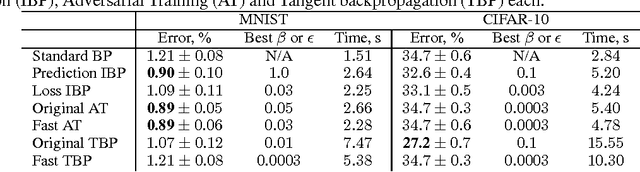
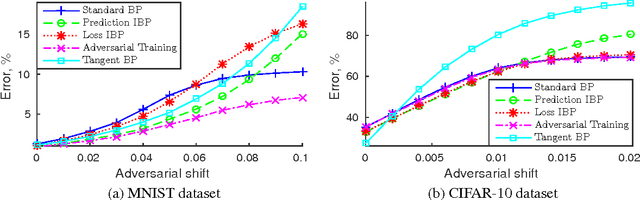
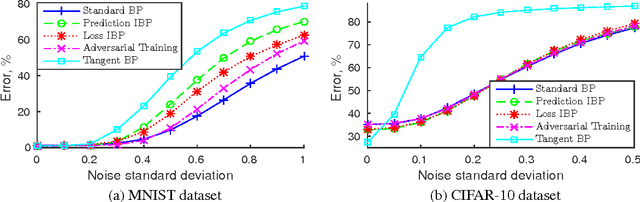
In many classification problems a classifier should be robust to small variations in the input vector. This is a desired property not only for particular transformations, such as translation and rotation in image classification problems, but also for all others for which the change is small enough to retain the object perceptually indistinguishable. We propose two extensions of the backpropagation algorithm that train a neural network to be robust to variations in the feature vector. While the first of them enforces robustness of the loss function to all variations, the second method trains the predictions to be robust to a particular variation which changes the loss function the most. The second methods demonstrates better results, but is slightly slower. We analytically compare the proposed algorithm with two the most similar approaches (Tangent BP and Adversarial Training), and propose their fast versions. In the experimental part we perform comparison of all algorithms in terms of classification accuracy and robustness to noise on MNIST and CIFAR-10 datasets. Additionally we analyze how the performance of the proposed algorithm depends on the dataset size and data augmentation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge