High-Order Optimization of Gradient Boosted Decision Trees

Gradient Boosted Decision Trees (GBDTs) are dominant machine learning algorithms for modeling discrete or tabular data. Unlike neural networks with millions of trainable parameters, GBDTs optimize loss function in an additive manner and have a single trainable parameter per leaf, which makes it easy to apply high-order optimization of the loss function. In this paper, we introduce high-order optimization for GBDTs based on numerical optimization theory which allows us to construct trees based on high-order derivatives of a given loss function. In the experiments, we show that high-order optimization has faster per-iteration convergence that leads to reduced running time. Our solution can be easily parallelized and run on GPUs with little overhead on the code. Finally, we discuss future potential improvements such as automatic differentiation of arbitrary loss function and combination of GBDTs with neural networks.

Towards OOD Detection in Graph Classification from Uncertainty Estimation Perspective

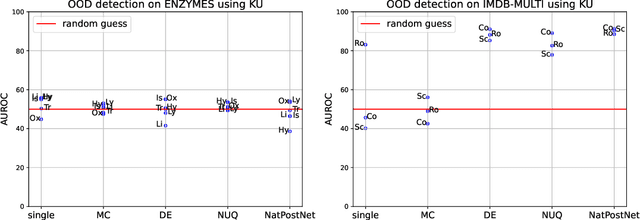
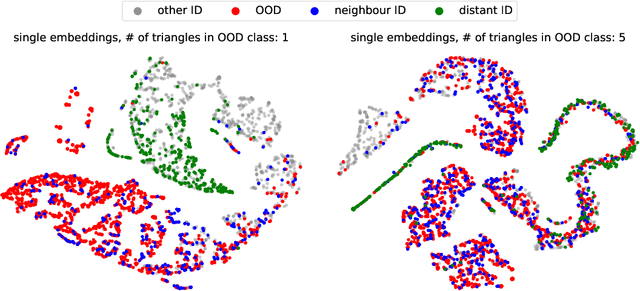
The problem of out-of-distribution detection for graph classification is far from being solved. The existing models tend to be overconfident about OOD examples or completely ignore the detection task. In this work, we consider this problem from the uncertainty estimation perspective and perform the comparison of several recently proposed methods. In our experiment, we find that there is no universal approach for OOD detection, and it is important to consider both graph representations and predictive categorical distribution.

High Performance of Gradient Boosting in Binding Affinity Prediction

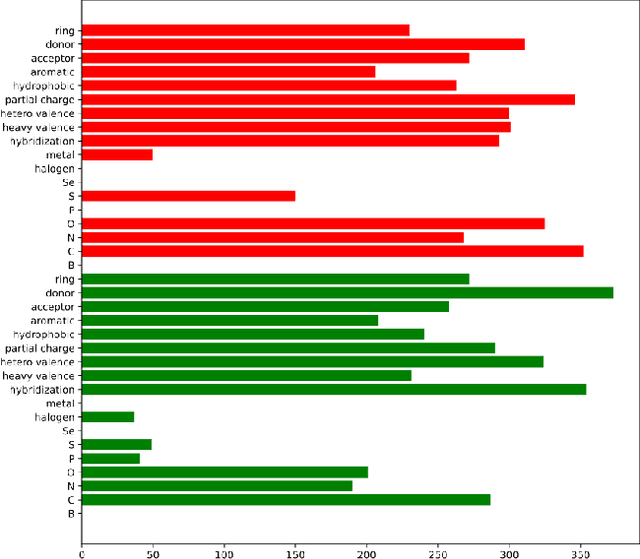
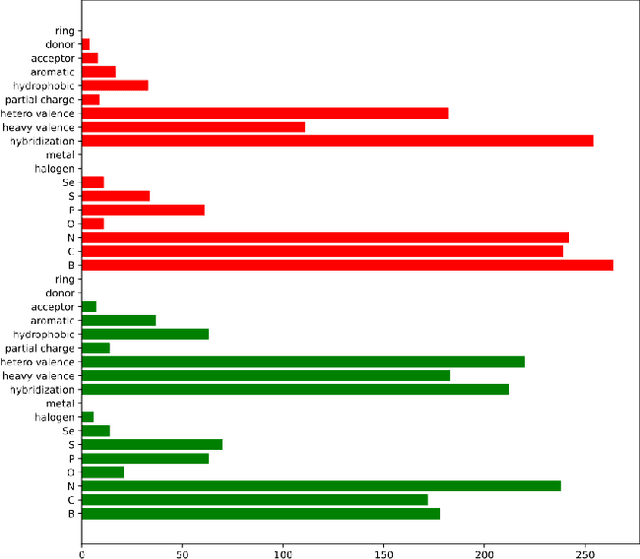
Prediction of protein-ligand (PL) binding affinity remains the key to drug discovery. Popular approaches in recent years involve graph neural networks (GNNs), which are used to learn the topology and geometry of PL complexes. However, GNNs are computationally heavy and have poor scalability to graph sizes. On the other hand, traditional machine learning (ML) approaches, such as gradient-boosted decision trees (GBDTs), are lightweight yet extremely efficient for tabular data. We propose to use PL interaction features along with PL graph-level features in GBDT. We show that this combination outperforms the existing solutions.

Boost then Convolve: Gradient Boosting Meets Graph Neural Networks

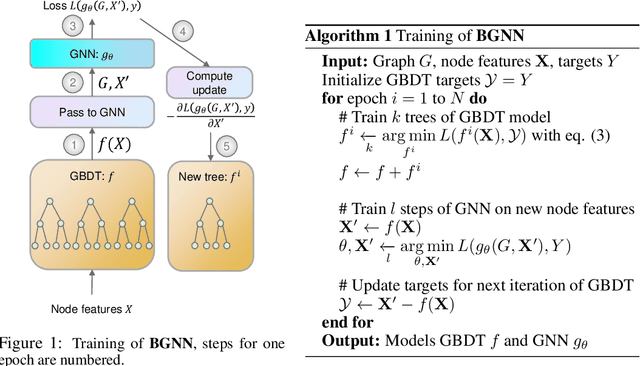
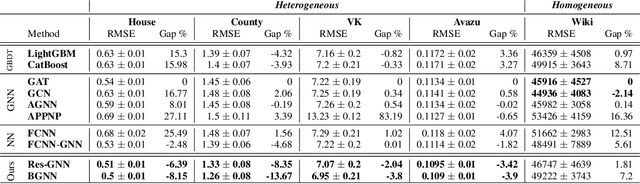
Graph neural networks (GNNs) are powerful models that have been successful in various graph representation learning tasks. Whereas gradient boosted decision trees (GBDT) often outperform other machine learning methods when faced with heterogeneous tabular data. But what approach should be used for graphs with tabular node features? Previous GNN models have mostly focused on networks with homogeneous sparse features and, as we show, are suboptimal in the heterogeneous setting. In this work, we propose a novel architecture that trains GBDT and GNN jointly to get the best of both worlds: the GBDT model deals with heterogeneous features, while GNN accounts for the graph structure. Our model benefits from end-to-end optimization by allowing new trees to fit the gradient updates of GNN. With an extensive experimental comparison to the leading GBDT and GNN models, we demonstrate a significant increase in performance on a variety of graphs with tabular features. The code is available: https://github.com/nd7141/bgnn.

Reinforcement Learning for Combinatorial Optimization: A Survey

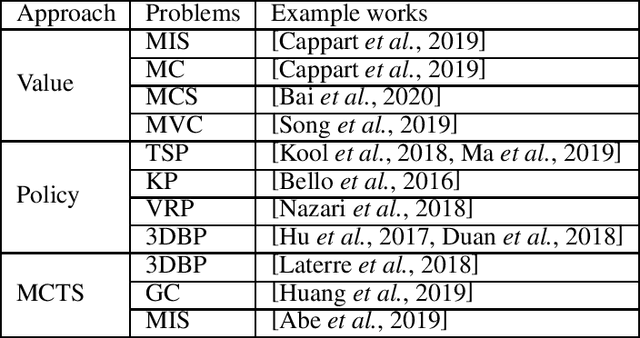
Combinatorial optimization (CO) is the workhorse of numerous important applications in operations research, engineering and other fields and, thus, has been attracting enormous attention from the research community for over a century. Many efficient solutions to common problems involve using hand-crafted heuristics to sequentially construct a solution. Therefore, it is intriguing to see how a combinatorial optimization problem can be formulated as a sequential decision making process and whether efficient heuristics can be implicitly learned by a reinforcement learning agent to find a solution. This survey explores the synergy between CO and reinforcement learning (RL) framework, which can become a promising direction for solving combinatorial problems.

Understanding Isomorphism Bias in Graph Data Sets

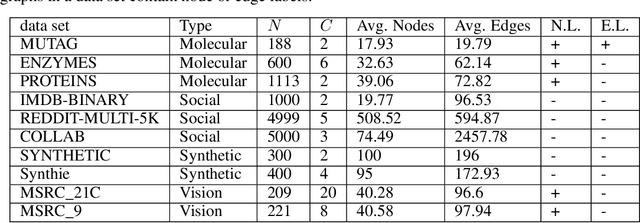
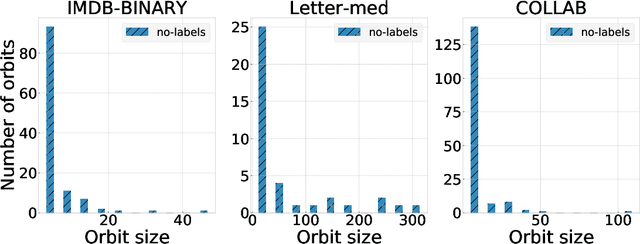
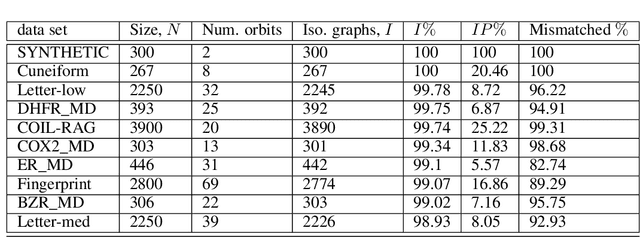
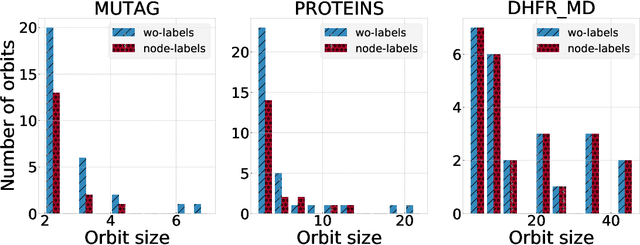
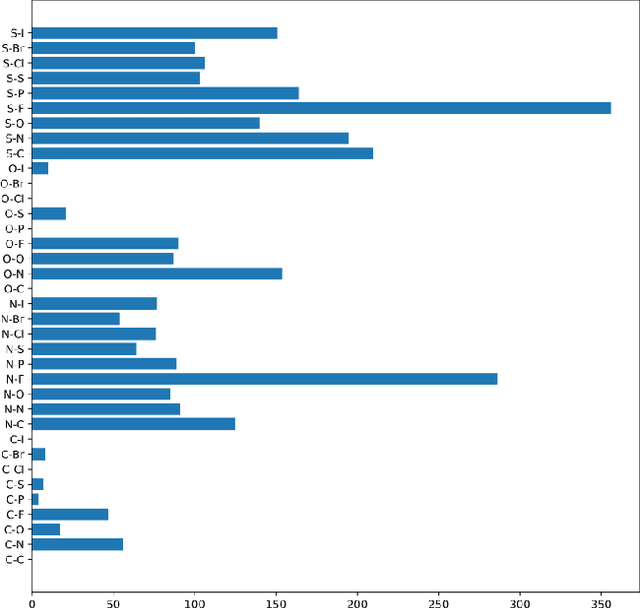
In recent years there has been a rapid increase in classification methods on graph structured data. Both in graph kernels and graph neural networks, one of the implicit assumptions of successful state-of-the-art models was that incorporating graph isomorphism features into the architecture leads to better empirical performance. However, as we discover in this work, commonly used data sets for graph classification have repeating instances which cause the problem of isomorphism bias, i.e. artificially increasing the accuracy of the models by memorizing target information from the training set. This prevents fair competition of the algorithms and raises a question of the validity of the obtained results. We analyze 54 data sets, previously extensively used for graph-related tasks, on the existence of isomorphism bias, give a set of recommendations to machine learning practitioners to properly set up their models, and open source new data sets for the future experiments.