Domain-Factored Untrained Deep Prior for Spectrum Cartography

Spectrum cartography (SC) focuses on estimating the radio power propagation map of multiple emitters across space and frequency using limited sensor measurements. Recent advances in SC have shown that leveraging learned deep generative models (DGMs) as structural constraints yields state-of-the-art performance. By harnessing the expressive power of neural networks, these structural "priors" capture intricate patterns in radio maps. However, training DGMs requires substantial data, which is not always available, and distribution shifts between training and testing data can further degrade performance. To address these challenges, this work proposes using untrained neural networks (UNNs) for SC. UNNs, commonly applied in vision tasks to represent complex data without training, encode structural information of data in neural architectures. In our approach, a custom-designed UNN represents radio maps under a spatio-spectral domain factorization model, leveraging physical characteristics to reduce sample complexity of SC. Experiments show that the method achieves performance comparable to learned DGM-based SC, without requiring training data.

Content-Style Learning from Unaligned Domains: Identifiability under Unknown Latent Dimensions

Understanding identifiability of latent content and style variables from unaligned multi-domain data is essential for tasks such as domain translation and data generation. Existing works on content-style identification were often developed under somewhat stringent conditions, e.g., that all latent components are mutually independent and that the dimensions of the content and style variables are known. We introduce a new analytical framework via cross-domain \textit{latent distribution matching} (LDM), which establishes content-style identifiability under substantially more relaxed conditions. Specifically, we show that restrictive assumptions such as component-wise independence of the latent variables can be removed. Most notably, we prove that prior knowledge of the content and style dimensions is not necessary for ensuring identifiability, if sparsity constraints are properly imposed onto the learned latent representations. Bypassing the knowledge of the exact latent dimension has been a longstanding aspiration in unsupervised representation learning -- our analysis is the first to underpin its theoretical and practical viability. On the implementation side, we recast the LDM formulation into a regularized multi-domain GAN loss with coupled latent variables. We show that the reformulation is equivalent to LDM under mild conditions -- yet requiring considerably less computational resource. Experiments corroborate with our theoretical claims.

Identifiable Shared Component Analysis of Unpaired Multimodal Mixtures

A core task in multi-modal learning is to integrate information from multiple feature spaces (e.g., text and audio), offering modality-invariant essential representations of data. Recent research showed that, classical tools such as {\it canonical correlation analysis} (CCA) provably identify the shared components up to minor ambiguities, when samples in each modality are generated from a linear mixture of shared and private components. Such identifiability results were obtained under the condition that the cross-modality samples are aligned/paired according to their shared information. This work takes a step further, investigating shared component identifiability from multi-modal linear mixtures where cross-modality samples are unaligned. A distribution divergence minimization-based loss is proposed, under which a suite of sufficient conditions ensuring identifiability of the shared components are derived. Our conditions are based on cross-modality distribution discrepancy characterization and density-preserving transform removal, which are much milder than existing studies relying on independent component analysis. More relaxed conditions are also provided via adding reasonable structural constraints, motivated by available side information in various applications. The identifiability claims are thoroughly validated using synthetic and real-world data.

Towards Identifiable Unsupervised Domain Translation: A Diversified Distribution Matching Approach

Unsupervised domain translation (UDT) aims to find functions that convert samples from one domain (e.g., sketches) to another domain (e.g., photos) without changing the high-level semantic meaning (also referred to as ``content''). The translation functions are often sought by probability distribution matching of the transformed source domain and target domain. CycleGAN stands as arguably the most representative approach among this line of work. However, it was noticed in the literature that CycleGAN and variants could fail to identify the desired translation functions and produce content-misaligned translations. This limitation arises due to the presence of multiple translation functions -- referred to as ``measure-preserving automorphism" (MPA) -- in the solution space of the learning criteria. Despite awareness of such identifiability issues, solutions have remained elusive. This study delves into the core identifiability inquiry and introduces an MPA elimination theory. Our analysis shows that MPA is unlikely to exist, if multiple pairs of diverse cross-domain conditional distributions are matched by the learning function. Our theory leads to a UDT learner using distribution matching over auxiliary variable-induced subsets of the domains -- other than over the entire data domains as in the classical approaches. The proposed framework is the first to rigorously establish translation identifiability under reasonable UDT settings, to our best knowledge. Experiments corroborate with our theoretical claims.

Quantized Radio Map Estimation Using Tensor and Deep Generative Models

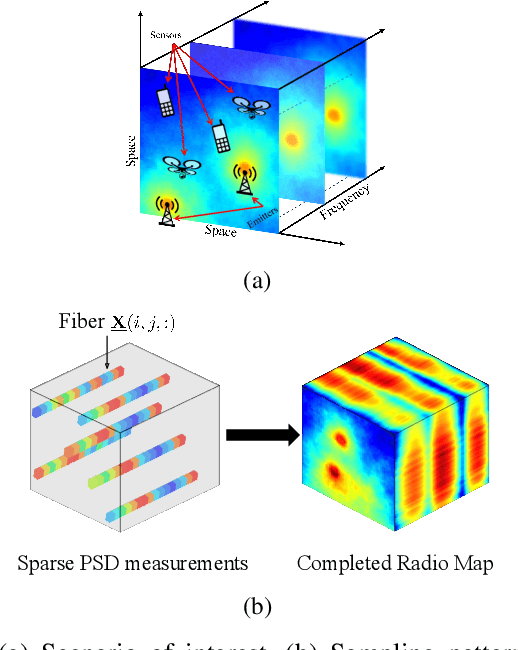
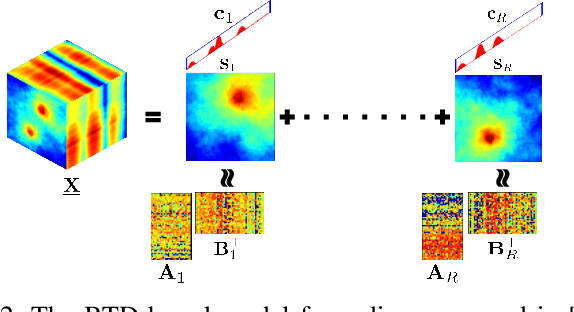
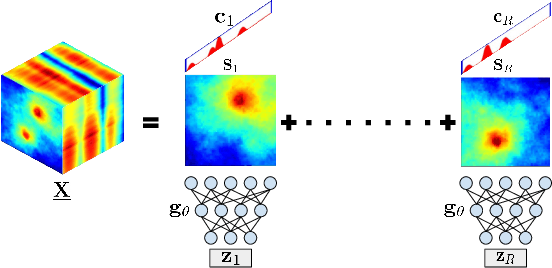
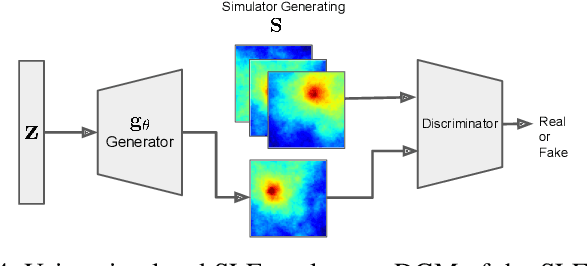
Spectrum cartography (SC), also known as radio map estimation (RME), aims at crafting multi-domain (e.g., frequency and space) radio power propagation maps from limited sensor measurements. While early methods often lacked theoretical support, recent works have demonstrated that radio maps can be provably recovered using low-dimensional models -- such as the block-term tensor decomposition (BTD) model and certain deep generative models (DGMs) -- of the high-dimensional multi-domain radio signals. However, these existing provable SC approaches assume that sensors send real-valued (full-resolution) measurements to the fusion center, which is unrealistic. This work puts forth a quantized SC framework that generalizes the BTD and DGM-based SC to scenarios where heavily quantized sensor measurements are used. A maximum likelihood estimation (MLE)-based SC framework under a Gaussian quantizer is proposed. Recoverability of the radio map using the MLE criterion are characterized under realistic conditions, e.g., imperfect radio map modeling and noisy measurements. Simulations and real-data experiments are used to showcase the effectiveness of the proposed approach.

Optimal Solutions for Joint Beamforming and Antenna Selection: From Branch and Bound to Machine Learning

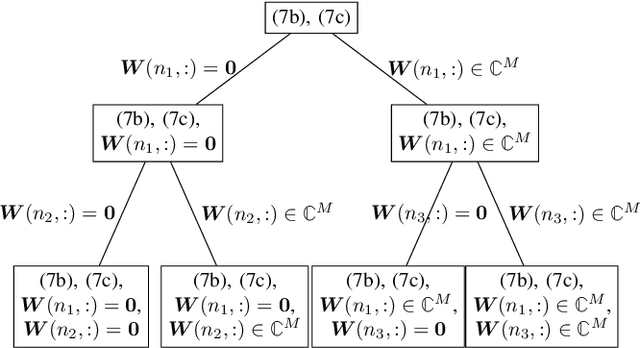
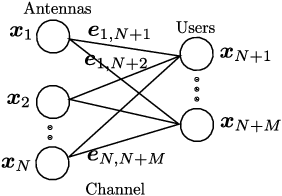
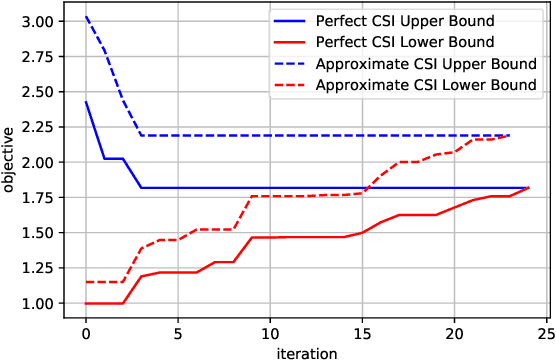
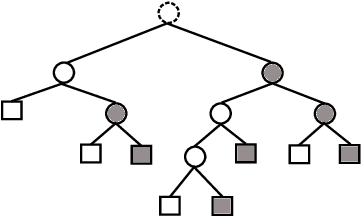
This work revisits the joint beamforming (BF) and antenna selection (AS) problem, as well as its robust beamforming (RBF) version under imperfect channel state information (CSI). Such problems arise in scenarios where the number of the radio frequency (RF) chains is smaller than that of the antenna elements at the transmitter, which has become a critical consideration in the era of large-scale arrays. The joint (R)BF\&AS problem is a mixed integer and nonlinear program, and thus finding {\it optimal solutions} is often costly, if not outright impossible. The vast majority of the prior works tackled these problems using continuous optimization-based approximations -- yet these approximations do not ensure optimality or even feasibility of the solutions. The main contribution of this work is threefold. First, an effective {\it branch and bound} (B\&B) framework for solving the problems of interest is proposed. Leveraging existing BF and RBF solvers, it is shown that the B\&B framework guarantees global optimality of the considered problems. Second, to expedite the potentially costly B\&B algorithm, a machine learning (ML)-based scheme is proposed to help skip intermediate states of the B\&B search tree. The learning model features a {\it graph neural network} (GNN)-based design that is resilient to a commonly encountered challenge in wireless communications, namely, the change of problem size (e.g., the number of users) across the training and test stages. Third, comprehensive performance characterizations are presented, showing that the GNN-based method retains the global optimality of B\&B with provably reduced complexity, under reasonable conditions. Numerical simulations also show that the ML-based acceleration can often achieve an order-of-magnitude speedup relative to B\&B.

Communication-Efficient Distributed Linear and Deep Generalized Canonical Correlation Analysis

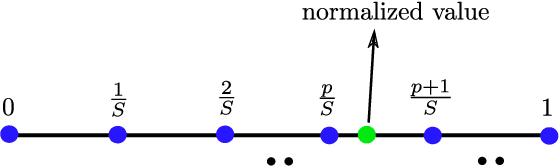
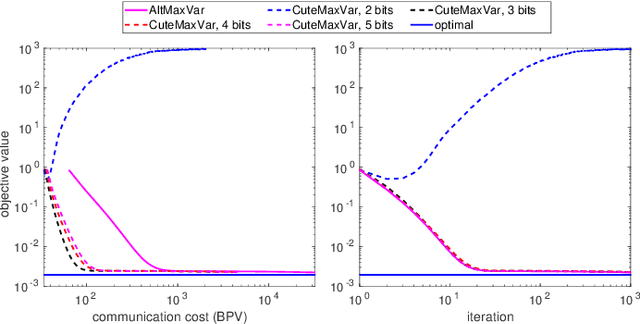
Classic and deep learning-based generalized canonical correlation analysis (GCCA) algorithms seek low-dimensional common representations of data entities from multiple ``views'' (e.g., audio and image) using linear transformations and neural networks, respectively. When the views are acquired and stored at different locations, organizations and edge devices, computing GCCA in a distributed, parallel and efficient manner is well-motivated. However, existing distributed GCCA algorithms may incur prohitively high communication overhead. This work puts forth a communication-efficient distributed framework for both linear and deep GCCA under the maximum variance (MAX-VAR) paradigm. The overhead issue is addressed by aggressively compressing (via quantization) the exchanging information between the distributed computing agents and a central controller. Compared to the unquantized version, the proposed algorithm consistently reduces the communication overhead by about $90\%$ with virtually no loss in accuracy and convergence speed. Rigorous convergence analyses are also presented -- which is a nontrivial effort since no existing generic result from quantized distributed optimization covers the special problem structure of GCCA. Our result shows that the proposed algorithms for both linear and deep GCCA converge to critical points in a sublinear rate, even under heavy quantization and stochastic approximations. In addition, it is shown that in the linear MAX-VAR case, the quantized algorithm approaches a {\it global optimum} in a {\it geometric} rate -- if the computing agents' updates meet a certain accuracy level. Synthetic and real data experiments are used to showcase the effectiveness of the proposed approach.

Deep Spectrum Cartography: Completing Radio Map Tensors Using Learned Neural Models

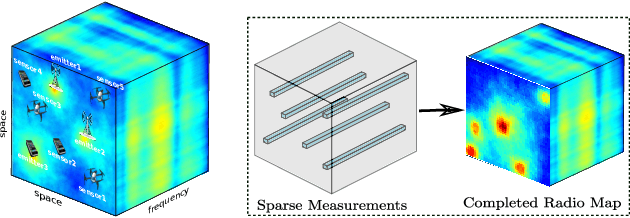
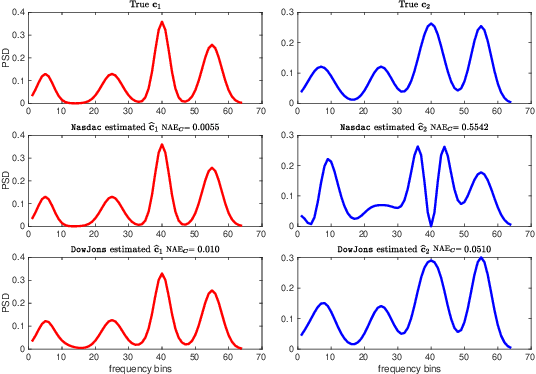
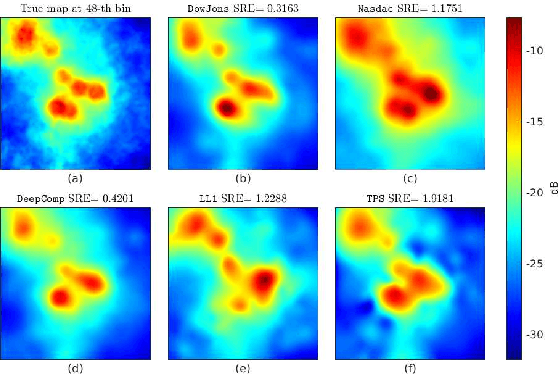
The spectrum cartography (SC) technique constructs multi-domain (e.g., frequency, space, and time) radio frequency (RF) maps from limited measurements, which can be viewed as an ill-posed tensor completion problem. Model-based cartography techniques often rely on handcrafted priors (e.g., sparsity, smoothness and low-rank structures) for the completion task. Such priors may be inadequate to capture the essence of complex wireless environments -- especially when severe shadowing happens. To circumvent such challenges, offline-trained deep neural models of radio maps were considered for SC, as deep neural networks (DNNs) are able to "learn" intricate underlying structures from data. However, such deep learning (DL)-based SC approaches encounter serious challenges in both off-line model learning (training) and completion (generalization), possibly because the latent state space for generating the radio maps is prohibitively large. In this work, an emitter radio map disaggregation-based approach is proposed, under which only individual emitters' radio maps are modeled by DNNs. This way, the learning and generalization challenges can both be substantially alleviated. Using the learned DNNs, a fast nonnegative matrix factorization-based two-stage SC method and a performance-enhanced iterative optimization algorithm are proposed. Theoretical aspects -- such as recoverability of the radio tensor, sample complexity, and noise robustness -- under the proposed framework are characterized, and such theoretical properties have been elusive in the context of DL-based radio tensor completion. Experiments using synthetic and real-data from indoor and heavily shadowed environments are employed to showcase the effectiveness of the proposed methods.