Quantized Radio Map Estimation Using Tensor and Deep Generative Models
Paper and Code
Mar 03, 2023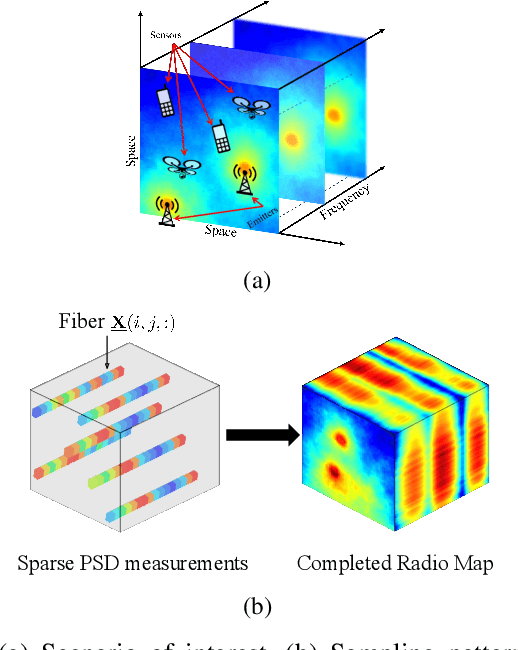
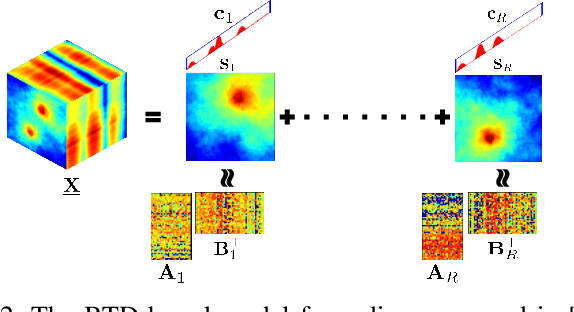
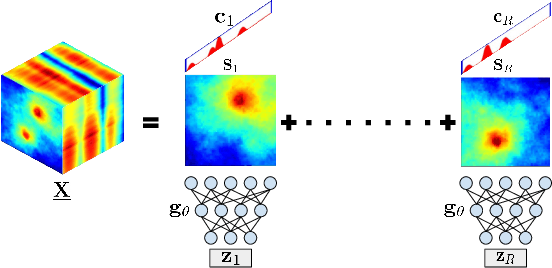
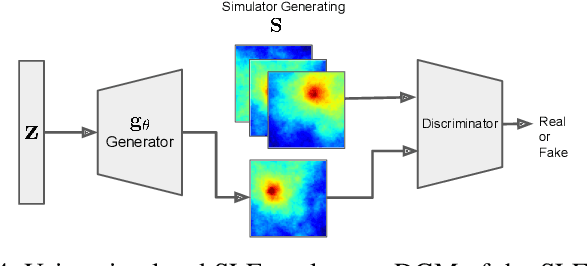
Spectrum cartography (SC), also known as radio map estimation (RME), aims at crafting multi-domain (e.g., frequency and space) radio power propagation maps from limited sensor measurements. While early methods often lacked theoretical support, recent works have demonstrated that radio maps can be provably recovered using low-dimensional models -- such as the block-term tensor decomposition (BTD) model and certain deep generative models (DGMs) -- of the high-dimensional multi-domain radio signals. However, these existing provable SC approaches assume that sensors send real-valued (full-resolution) measurements to the fusion center, which is unrealistic. This work puts forth a quantized SC framework that generalizes the BTD and DGM-based SC to scenarios where heavily quantized sensor measurements are used. A maximum likelihood estimation (MLE)-based SC framework under a Gaussian quantizer is proposed. Recoverability of the radio map using the MLE criterion are characterized under realistic conditions, e.g., imperfect radio map modeling and noisy measurements. Simulations and real-data experiments are used to showcase the effectiveness of the proposed approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge