Communication-Efficient Distributed Linear and Deep Generalized Canonical Correlation Analysis
Paper and Code
Sep 25, 2021
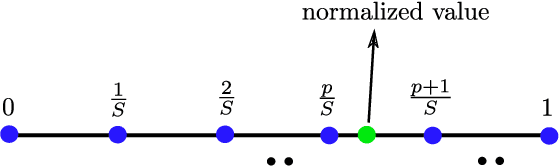

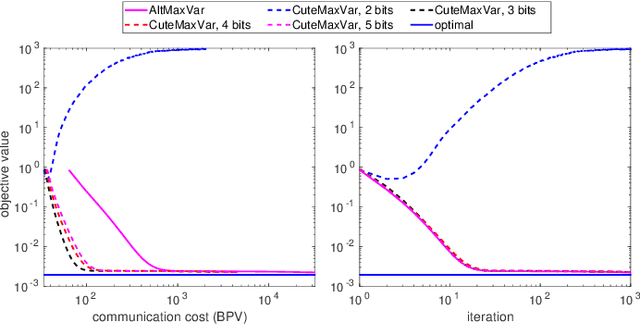
Classic and deep learning-based generalized canonical correlation analysis (GCCA) algorithms seek low-dimensional common representations of data entities from multiple ``views'' (e.g., audio and image) using linear transformations and neural networks, respectively. When the views are acquired and stored at different locations, organizations and edge devices, computing GCCA in a distributed, parallel and efficient manner is well-motivated. However, existing distributed GCCA algorithms may incur prohitively high communication overhead. This work puts forth a communication-efficient distributed framework for both linear and deep GCCA under the maximum variance (MAX-VAR) paradigm. The overhead issue is addressed by aggressively compressing (via quantization) the exchanging information between the distributed computing agents and a central controller. Compared to the unquantized version, the proposed algorithm consistently reduces the communication overhead by about $90\%$ with virtually no loss in accuracy and convergence speed. Rigorous convergence analyses are also presented -- which is a nontrivial effort since no existing generic result from quantized distributed optimization covers the special problem structure of GCCA. Our result shows that the proposed algorithms for both linear and deep GCCA converge to critical points in a sublinear rate, even under heavy quantization and stochastic approximations. In addition, it is shown that in the linear MAX-VAR case, the quantized algorithm approaches a {\it global optimum} in a {\it geometric} rate -- if the computing agents' updates meet a certain accuracy level. Synthetic and real data experiments are used to showcase the effectiveness of the proposed approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge