Optimal Solutions for Joint Beamforming and Antenna Selection: From Branch and Bound to Machine Learning
Paper and Code
Jun 11, 2022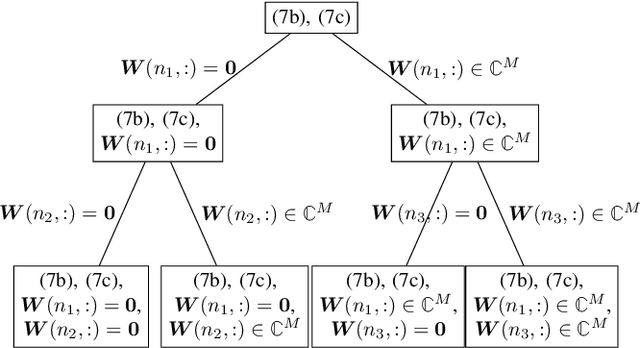
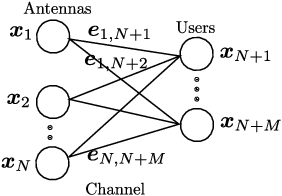
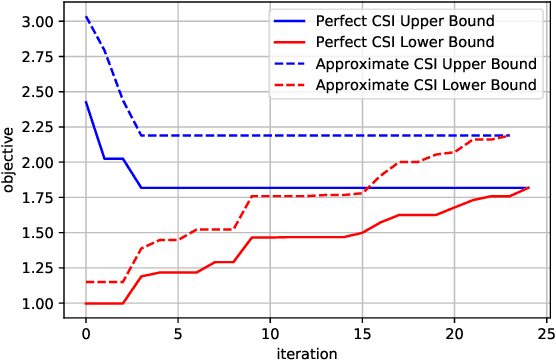
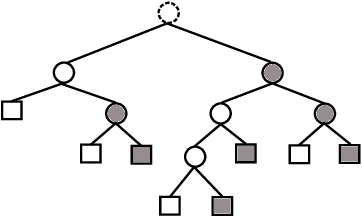
This work revisits the joint beamforming (BF) and antenna selection (AS) problem, as well as its robust beamforming (RBF) version under imperfect channel state information (CSI). Such problems arise in scenarios where the number of the radio frequency (RF) chains is smaller than that of the antenna elements at the transmitter, which has become a critical consideration in the era of large-scale arrays. The joint (R)BF\&AS problem is a mixed integer and nonlinear program, and thus finding {\it optimal solutions} is often costly, if not outright impossible. The vast majority of the prior works tackled these problems using continuous optimization-based approximations -- yet these approximations do not ensure optimality or even feasibility of the solutions. The main contribution of this work is threefold. First, an effective {\it branch and bound} (B\&B) framework for solving the problems of interest is proposed. Leveraging existing BF and RBF solvers, it is shown that the B\&B framework guarantees global optimality of the considered problems. Second, to expedite the potentially costly B\&B algorithm, a machine learning (ML)-based scheme is proposed to help skip intermediate states of the B\&B search tree. The learning model features a {\it graph neural network} (GNN)-based design that is resilient to a commonly encountered challenge in wireless communications, namely, the change of problem size (e.g., the number of users) across the training and test stages. Third, comprehensive performance characterizations are presented, showing that the GNN-based method retains the global optimality of B\&B with provably reduced complexity, under reasonable conditions. Numerical simulations also show that the ML-based acceleration can often achieve an order-of-magnitude speedup relative to B\&B.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge