Iterative energy-based projection on a normal data manifold for anomaly localization

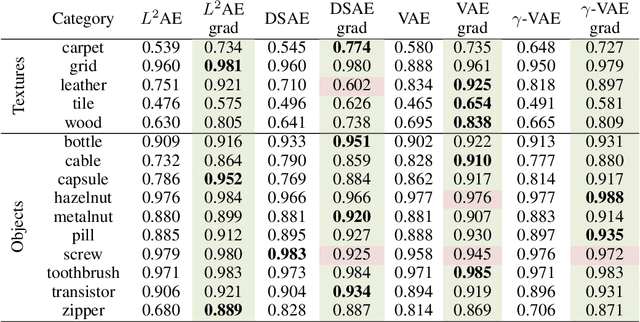
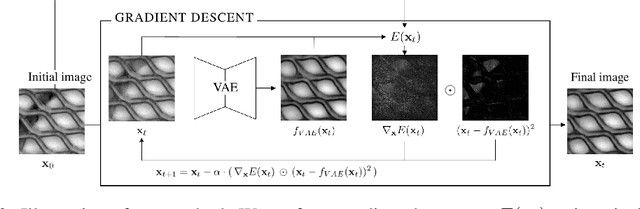
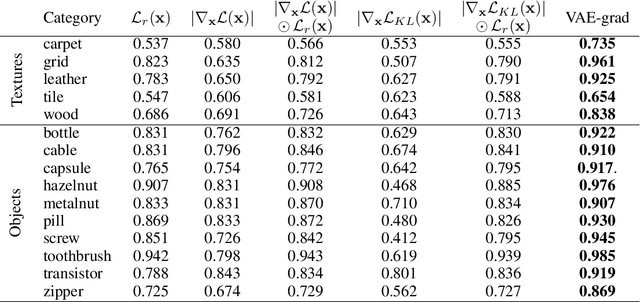
Autoencoder reconstructions are widely used for the task of unsupervised anomaly localization. Indeed, an autoencoder trained on normal data is expected to only be able to reconstruct normal features of the data, allowing the segmentation of anomalous pixels in an image via a simple comparison between the image and its autoencoder reconstruction. In practice however, local defects added to a normal image can deteriorate the whole reconstruction, making this segmentation challenging. To tackle the issue, we propose in this paper a new approach for projecting anomalous data on a autoencoder-learned normal data manifold, by using gradient descent on an energy derived from the autoencoder's loss function. This energy can be augmented with regularization terms that model priors on what constitutes the user-defined optimal projection. By iteratively updating the input of the autoencoder, we bypass the loss of high-frequency information caused by the autoencoder bottleneck. This allows to produce images of higher quality than classic reconstructions. Our method achieves state-of-the-art results on various anomaly localization datasets. It also shows promising results at an inpainting task on the CelebA dataset.

Bayesian estimation of the multifractality parameter for image texture using a Whittle approximation

Texture characterization is a central element in many image processing applications. Multifractal analysis is a useful signal and image processing tool, yet, the accurate estimation of multifractal parameters for image texture remains a challenge. This is due in the main to the fact that current estimation procedures consist of performing linear regressions across frequency scales of the two-dimensional (2D) dyadic wavelet transform, for which only a few such scales are computable for images. The strongly non-Gaussian nature of multifractal processes, combined with their complicated dependence structure, makes it difficult to develop suitable models for parameter estimation. Here, we propose a Bayesian procedure that addresses the difficulties in the estimation of the multifractality parameter. The originality of the procedure is threefold: The construction of a generic semi-parametric statistical model for the logarithm of wavelet leaders; the formulation of Bayesian estimators that are associated with this model and the set of parameter values admitted by multifractal theory; the exploitation of a suitable Whittle approximation within the Bayesian model which enables the otherwise infeasible evaluation of the posterior distribution associated with the model. Performance is assessed numerically for several 2D multifractal processes, for several image sizes and a large range of process parameters. The procedure yields significant benefits over current benchmark estimators in terms of estimation performance and ability to discriminate between the two most commonly used classes of multifractal process models. The gains in performance are particularly pronounced for small image sizes, notably enabling for the first time the analysis of image patches as small as 64x64 pixels.