Iterative energy-based projection on a normal data manifold for anomaly localization
Paper and Code
Feb 10, 2020
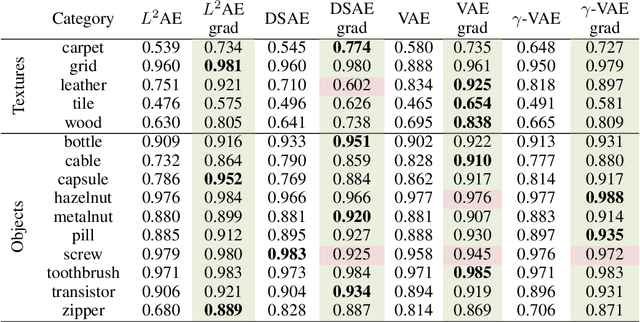
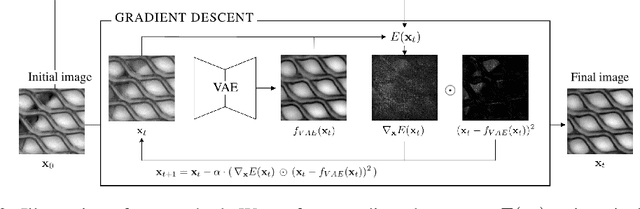
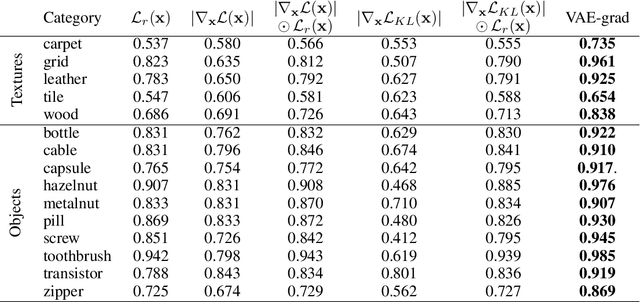
Autoencoder reconstructions are widely used for the task of unsupervised anomaly localization. Indeed, an autoencoder trained on normal data is expected to only be able to reconstruct normal features of the data, allowing the segmentation of anomalous pixels in an image via a simple comparison between the image and its autoencoder reconstruction. In practice however, local defects added to a normal image can deteriorate the whole reconstruction, making this segmentation challenging. To tackle the issue, we propose in this paper a new approach for projecting anomalous data on a autoencoder-learned normal data manifold, by using gradient descent on an energy derived from the autoencoder's loss function. This energy can be augmented with regularization terms that model priors on what constitutes the user-defined optimal projection. By iteratively updating the input of the autoencoder, we bypass the loss of high-frequency information caused by the autoencoder bottleneck. This allows to produce images of higher quality than classic reconstructions. Our method achieves state-of-the-art results on various anomaly localization datasets. It also shows promising results at an inpainting task on the CelebA dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge